2018年高考数学考试大纲说明(理科)
编辑:
2018-05-17
Ⅱ.考试范围与要求
本部分包括必考内容和选考内容两部分.必考内容为《课程标准》的必修内容和选修系列2的内容;选考内容为《课程标准》的选修系列4的“坐标系与参数方程”“不等式选讲”2个专题.
必考内容
(一)集合
1.集合的含义与表示
(1)了解集合的含义、元素与集合的属于关系.
(2)能用自然语言、图形语言、集合语言(列举法或描述法)描述不同的具体问题.
2.集合间的基本关系
(1)理解集合之间包含与相等的含义,能识别给定集合的子集.
(2)在具体情境中,了解全集与空集的含义.
3.集合的基本运算
(1)理解两个集合的并集与交集的含义,会求两个简单集合的并集与交集.
(2)理解在给定集合中一个子集的补集的含义,会求给定子集的补集.
(3)能使用韦恩(Venn)图表达集合的关系及运算.
(二)函数概念与基本初等函数Ⅰ(指数函数、对数函数、幂函数)
1.函数
(1)了解构成函数的要素,会求一些简单函数的定义域和值域;了解映射的概念.
(2)在实际情境中,会根据不同的需要选择恰当的方法(如图像法、列表法、解析法)表示函数.
(3)了解简单的分段函数,并能简单应用.
(4)理解函数的单调性、最大值、最小值及其几何意义;结合具体函数,了解函数奇偶性的含义.
(5)会运用函数图像理解和研究函数的性质.
2.指数函数
(1)了解指数函数模型的实际背景.
(2)理解有理指数幂的含义,了解实数指数幂的意义,掌握幂的运算.
(3)理解指数函数的概念,理解指数函数的单调性,掌握指数函数图像通过的特殊点.
(4)知道指数函数是一类重要的函数模型.
3.对数函数
(1)理解对数的概念及其运算性质,知道用换底公式能将一般对数转化成自然对数或常用对数;了解对数在简化运算中的作用.
(2)理解对数函数的概念,理解对数函数的单调性,掌握对数函数图像通过的特殊点.
(3)知道对数函数是一类重要的函数模型.
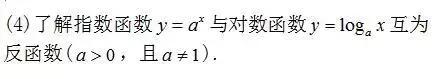
4.幂函数
(1)了解幂函数的概念.
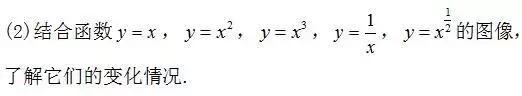
5.函数与方程
(1)结合二次函数的图像,了解函数的零点与方程根的联系,判断一元二次方程根的存在性及根的个数.
(2)根据具体函数的图像,能够用二分法求相应方程的近似解.
6.函数模型及其应用
(1)了解指数函数、对数函数以及幂函数的增长特征,知道直线上升、指数增长、对数增长等不同函数类型增长的含义.
(2)了解函数模型(如指数函数、对数函数、幂函数、分段函数等在社会生活中普遍使用的函数模型)的广泛应用.
标签:高考大纲说明
免责声明
精品学习网(51edu.com)在建设过程中引用了互联网上的一些信息资源并对有明确来源的信息注明了出处,版权归原作者及原网站所有,如果您对本站信息资源版权的归属问题存有异议,请您致信qinquan#51edu.com(将#换成@),我们会立即做出答复并及时解决。如果您认为本站有侵犯您权益的行为,请通知我们,我们一定根据实际情况及时处理。