要想让自己在考试时取得好成绩，除了上课要认真听讲外还需要课后多做练习，接下来精品学习网为大家推荐了正切函数随堂练习，希望能帮助到大家。

【素质优化训练】

1.解不等式3tan2(2x-

)-(3-

)tan(2x-

)-

≤0.

2.已知函数f(x)=tan(ωx+φ),且对于定义域内任何实数x，都有f(x)=f(x+1)-f(x+2),比较tan(ωa+φ+3ω)与tan(ωa+φ-3ω)的大小.

3.已知有两个函数f1(x)=αsin(kx+

),f2(x)=bsin(kx-

)(k>0)它们的最小正周期之和为2π，且f1(

)=f2(

),f1(

)=-

f2(

)+1,求a、b、k之值.

4.已知关于x的一元二次方程4x2+5x+k=0的两根分别为sinθ、cosθ,(1)求k.(2)求以tanθ、cotθ为两根的一元二次方程.

5.求证：函数y=Atan(ωx+φ)(Aω≠0)为奇函数的充要条件是φ=kπ(k∈Z).

【生活实际运用】

A、B、C是一条直路上的三点，AB与BC各等于1千米，从三点分别遥望塔M，在A处见塔在东北方向，在B处见塔在正东方向，在C处见塔在南偏东60°，求塔与路的最短距离.

分析：求塔与路的距离MD的最小值，在引入参变量角θ以后，主要是找参变量θ和MD的关系式，也就是将MD表示成θ的函数，注意到BD、DA与MD的联系时，建立三角函数模型就不困难了.

解：如图所示，设塔到路的距离MD为x千米，∠BMD=θ，则∠CMD=30°+θ,∠AMD=45°-θ,AB=BD+DA=xtanθ+xtan(45°-θ),

BC=CD-BD=xtan(30°+θ)-xtanθ.

∵AB=BC=1,∴xtanθ+xtan(45°-θ)=xtan(30°+θ)-xtanθ=1.

x=

=

.

那么x=

=

,

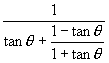
即

=

.

∴tanθ=

.

因此x=

=

=

千米.

即塔与路的最短距离是

千米.

有了上文为大家推荐的正切函数随堂练习，是不是助力不少呢?祝您学习愉快。

相关推荐：

高二数学下册《向量的数量积》同步测试  

苏教版高二数学下册《二倍角的三角函数》练习题及答案