同学们都在忙碌地复习自己的功课，为了帮助大家能够在考前对自己多学的知识点有所巩固，下文整理了这篇数学试题及答案，希望可以帮助到大家!

2013年清华等五校自主招生英语试题及答案

1.以

和

为两根的有理系数多项式的次数最小是多少?

 

A.2　　　B.3　　C.5　　D.6

解析：显然

为满足要求的多项式，其次数为5.

 

若存在

次有理系数多项式

以

和

为两根，则

必含有因式

，∴

，即最小次数为5.故选C.

 

2.在

的棋盘中停放着3个红色車和3个黑色車，每一行、每一列都只有一个車，共有多少种停放方法?

 

A.720　　　B.20　　C.518400　　D.14400

解析：先排3个红色車，从6行中任取3行，有

种取法;在选定的3行中第一行有6种停法，第一行选定后第二行有5种停法，第二行选定后第三行有4种停法;红車放定后，黑車只有6种停法.故停放方法共

种.故选D.

 

3.已知

，

，求

的值.

 

解析： ∵

，

 

又由

，

，有

∴

或

.

 

当

时，有

，

，

 

;

 

当

时，

，

.

 

4.如图，△ABC中，AD为BC边上的中线，DM、DN分别为∠ADB、∠ADC的角平分线，试比较BM+CN与MN的大小关系，并说明理由.

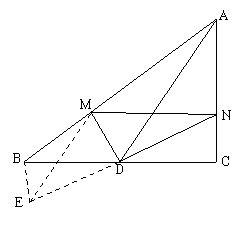
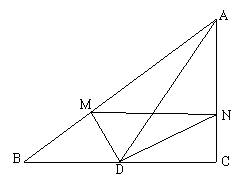
解析：延长ND至E，使ND=ED，连结BE、ME，

则△BED≌△CND，△MED≌△MND，ME=MN，

由BM+BE>EM，得BM+CN>MN.

5.设数列

满足

，前

项和为

，

，求

.

 

解析： ∵

，

，∴

;

 

由 

，有

时，

，于是

，

 

特征方程

有重根2，可设

，

 

将

，

代入上式，得

，

，

 

于是

，∴

.

 

6.模长为1的复数

满足

，求

.

 

解析：取

，便能得到

=1.

 

下面给出证明，

，

 

于是

.∴

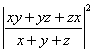
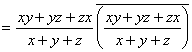
=1.

 

7.最多有多少个两两不等的正整数，满足其中任意三数之和都为素数.

解析：设满足条件的正整数为

个.考虑模3的同余类，共三类，记为

，

，

.

 

则这

个正整数需同时满足①不能三类都有;②同一类中不能有3个和超过3个.否则都会出现三数之和为3的倍数.故

.

 

当

时，取1，3，7，9，其任意三数之和为11，13，17，19均为素数，满足题意，所以满足要求的正整数最多有4个.

 

8.已知

，

为2013个实数，满足

，且

…

，求证

.

 

解析：设

…

，

 

若

，则

，

，…，

，

，

 

于是

，

 

∴

，进而

.

 

若

，则

，

，…，

 这2013个数去掉绝对值号后只能取

和

两值，

 

又

…

，

 

即这2013个数去掉绝对值号后取

和

两值的个数相同，这不可能.

 

9.对于任意的

，求

的值.

 

解析：

，

 

，

 

，

 

，

 

各式相加，得

.

 

10.已知有

个实数，排列成

阶数阵，记作

使得数阵的每一行从左到右都是递增的，即对任意的

，当

时，有

;现将

的每一列原有的各数按照从上到下递增的顺序排列，形成一个新的

阶数阵，记作

，即对任意的

，当

时，有

，试判断

中每一行的各数的大小关系，并加以证明.

 

解析：数阵

中的中每一行的各数仍是递增的.下面用反证法给出证明.

 

若在第

行存在

，令

，其中

，

 

，则当

时，

即在第

列中至少有

个数小于

，也就是

在数阵

中的第

列中至少排在第

行，这与

排在第

行矛盾.所以数阵

中的中每一行的各数仍是递增的.

这篇数学试题及答案就为大家分享到这里了。希望对大家有所帮助！

相关推荐：

广东省东莞市2014届高三模拟（一）数学理试题