高中数学重点知识：如何求参数的取值范围

【摘要】高中学生在学习中或多或少有一些困惑，精品学习网的编辑为大家总结了高中数学重点知识：如何求参数的取值范围，各位考生可以参考。

资源名称：高考难点：如何求参数的取值范围

资源分类：高考复习教案

资源版本：人教版

文件类型：doc

资源大小：200kb

下载地址：高考难点：如何求参数的取值范围

资源简介：

一、通过解关于a，c的二元齐次不等式求离心率的范围

例1 已知、F1,F2是椭圆的两个焦点，满足

的点总在椭圆的内部，则椭圆离心率的取值范围是

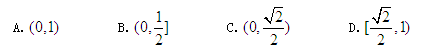
解据题意可知，∠M是直角，则垂足M的轨迹是以焦距为直径的圆.所以.又，所以.选C.

小结本题是最常见的求离心率范围的问题，其方法就是根据已知条件，直接列出关于a，b，c间的不等量关系，然后利用a，b，c间的平方关系化为关于a，c的齐次不等式，除以即为关于离心率e的一元二次不等式，解不等式，再结合椭圆或双曲线的离心率的范围，就得到了离心率的取值范围.

二、利用一元二次方程的判别式求参数的范围

例2 直线y=kx+2与椭圆至多有一个交点的充要条件是

解将直线方程代入椭圆方程，得.由，解得.选A.

小结本题表面上看是一个充要条件问题，但其实质仍然是求参数k的取值范围.对于直线与圆锥曲线的交点问题，一般都是将直线方程代入曲线方程，利用一元二次方程判别式来求解，这是最基本的思路和方法.但需要引起同学们重视的是，当一元二次方程的二次项系数含参数时需分类讨论.对于双曲线，还需结合图像来讨论，否则很容易出错.

以上就是高中数学重点知识：如何求参数的取值范围的全部内容，更多考试资讯请继续关注精品学习网!

相关推荐

高一数学知识点：一次函数