2014高一数学对数函数教案
编辑:
2014-08-27
一. 引入新课
今天我们一起再来研究一种常见函数.前面的几种函数都是以形式定义的方式给出的,今天我们将从反函数的角度介绍新的函数.
反函数的实质是研究两个函数的关系,所以自然我们应从大家熟悉的函数出发,再研究其反函数.这个熟悉的函数就是指数函数.
提问:什么是指数函数?指数函数存在反函数吗?
由学生说出
![]()
是指数函数,它是存在反函数的.并由一个学生口答求反函数的过程:
由
![]()
得
![]()
.又
![]()
的值域为
![]()
,
![]()
所求反函数为
![]()
![]()
.
那么我们今天就是研究指数函数的反函数-----对数函数.
2.8对数函数 (板书)
一. 对数函数的概念
1. 定义:函数
![]()
的反函数
![]()
叫做对数函数.
由于定义就是从反函数角度给出的,所以下面我们的研究就从这个角度出发.如从定义中你能了解对数函数的什么性质吗?最初步的认识是什么?
教师可提示学生从反函数的三定与三反去认识,从而找出对数函数的定义域为
![]()
,对数函数的值域为
![]()
,且底数
![]()
就是指数函数中的
![]()
,故有着相同的限制条件
![]()
.
在此基础上,我们将一起来研究对数函数的图像与性质.
二.对数函数的图像与性质 (板书)
1. 作图方法
提问学生打算用什么方法来画函数图像?学生应能想到利用互为反函数的两个函数图像之间的关系,利用图像变换法画图.同时教师也应指出用列表描点法也是可以的,让学生从中选出一种,最终确定用图像变换法画图.
由于指数函数的图像按
![]()
和
![]()
分成两种不同的类型,故对数函数的图像也应以1为分界线分成两种情况
![]()
和
![]()
,并分别以
![]()
和
![]()
为例画图.
具体操作时,要求学生做到:
(1) 指数函数
![]()
和
![]()
的图像要尽量准确(关键点的位置,图像的变化趋势等).
(2) 画出直线
![]()
.
(3)
![]()
的图像在翻折时先将特殊点
![]()
对称点
![]()
找到,变化趋势由靠近
![]()
轴对称为逐渐靠近
![]()
轴,而
![]()
的图像在翻折时可提示学生分两段翻折,在
![]()
左侧的先翻,然后再翻在
![]()
右侧的部分.
学生在笔记本完成具体操作,教师在学生完成后将关键步骤在黑板上演示一遍,画出
![]()
和
![]()
的图像.(此时同底的指数函数和对数函数画在同一坐标系内)如图:
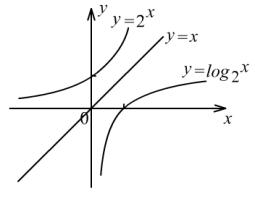
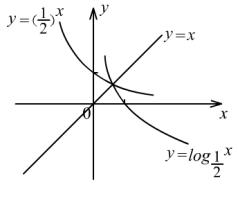
2. 草图.
教师画完图后再利用投影仪将
![]()
和
![]()
的图像画在同一坐标系内,如图:
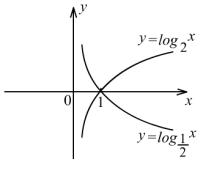
然后提出让学生根据图像说出对数函数的性质(要求从几何与代数两个角度说明)
3. 性质
(1) 定义域:
![]()
(2) 值域:
![]()
由以上两条可说明图像位于
![]()
轴的右侧.
(3) 截距:令
![]()
得
![]()
,即在
![]()
轴上的截距为1,与
![]()
轴无交点即以
![]()
轴为渐近线.
(4) 奇偶性:既不是奇函数也不是偶函数,即它不关于原点对称,也不关于
![]()
轴对称.
(5) 单调性:与
![]()
有关.当
![]()
时,在
![]()
上是增函数.即图像是上升的
当
![]()
时,在
![]()
上是减函数,即图像是下降的.
之后可以追问学生有没有最大值和最小值,当得到否定答案时,可以再问能否看待何时函数值为正?学生看着图可以答出应有两种情况:
当
![]()
时,有
![]()
;当
![]()
时,有
![]()
.
学生回答后教师可指导学生巧记这个结论的方法:当底数与真数在1的同侧时函数值为正,当底数与真数在1的两侧时,函数值为负,并把它当作第(6)条性质板书记下来.
最后教师在总结时,强调记住性质的关键在于要脑中有图.且应将其性质与指数函数的性质对比记忆.(特别强调它们单调性的一致性)
对图像和性质有了一定的了解后,一起来看看它们的应用.
标签:高一数学教案
免责声明
精品学习网(51edu.com)在建设过程中引用了互联网上的一些信息资源并对有明确来源的信息注明了出处,版权归原作者及原网站所有,如果您对本站信息资源版权的归属问题存有异议,请您致信qinquan#51edu.com(将#换成@),我们会立即做出答复并及时解决。如果您认为本站有侵犯您权益的行为,请通知我们,我们一定根据实际情况及时处理。