【摘要】精品学习网的编辑就为各位学生带来了高中高一数学必修5教学设计。

高中高一数学必修5教学设计：《1.1.1 正弦定理》教学设计

一、教学内容分析

“正弦定理”是《普通高中课程标准数学教科书·数学(必修5)》(人教版)第一章第一节的主要内容，它既是初中“解直角三角形”内容的直接延拓，也是三角函数一般知识和平面向量等知识在三角形中的具体运用，是解可转化为三角形计算问题的其它数学问题及生产、生活实际问题的重要工具，因此具有广泛的应用价值。为什么要研究正弦定理?正弦定理是怎样发现的?其证明方法是怎样想到的?还有别的证法吗?这些都是教材没有回答，而确实又是学生所关心的问题。

本节课是“正弦定理”教学的第一课时，其主要任务是引入并证明正弦定理，在课型上属于“定理教学课”。因此，做好“正弦定理”的教学，不仅能复习巩固旧知识，使学生掌握新的有用的知识，体会联系、发展等辩证观点，而且通过对定理的探究，能使学生体验到数学发现和创造的历程，进而培养学生提出问题、解决问题等研究性学习的能力。

二、学生学习情况分析

学生在初中已经学习了解直角三角形的内容，在必修4中，又学习了三角函数的基础知识和平面向量的有关内容，对解直角三角形、三角函数、平面向量已形成初步的知识框架，这不仅是学习正弦定理的认知基础，同时又是突破定理证明障碍的强有力的工具。正弦定理是关于任意三角形边角关系的重要定理之一，《课程标准》强调在教学中要重视定理的探究过程，并能运用它解决一些实际问题，可以使学生进一步了解数学在实际中的应用，从而激发学生学习数学的兴趣，也为学习正弦定理提供一种亲和力与认同感。

三、设计思想

培养学生学会学习、学会探究是全面发展学生能力的重要前提，是高中新课程改革的主要任务。如何培养学生学会学习、学会探究呢?建构主义认为：“知识不是被动吸收的，而是由认知主体主动建构的。”这个观点从教学的角度来理解就是：知识不是通过教师传授得到的，而是学生在一定的情境中，运用已有的学习经验，并通过与他人(在教师指导和学习伙伴的帮助下)协作，主动建构而获得的，建构主义教学模式强调以学生为中心，视学生为认知的主体，教师只对学生的意义建构起帮助和促进作用。本节“正弦定理”的教学，将遵循这个原则而进行设计。

四、教学目标

1、知识与技能：通过对任意三角形的边与其对角的关系的探索，掌握正弦定理的内容及其证明方法。

2、过程与方法：让学生从已有的知识出发,共同探究在任意三角形中，边与其对角的关系，引导学生通过观察、归纳、猜想、证明，由特殊到一般得到正弦定理等方法，体验数学发现和创造的历程。

3、情感态度与价值观：在平等的教学氛围中，通过学生之间、师生之间的交流、合作和评价，实现共同探究、教学相长的教学情境。

五、教学重点与难点

重点：正弦定理的发现和推导

难点：正弦定理的推导

教学准备：制作多媒体课件，学生准备计算器，直尺，量角器。

六、教学过程设计

（一）设置情境

教师：展示情景图如图1，船从港口B航行到港口C，测得BC的距离为

，船在港口C卸货后继续向港口A航行，由于船员的疏忽没有测得CA距离，如果船上有测角仪我们能否计算出A、B的距离?

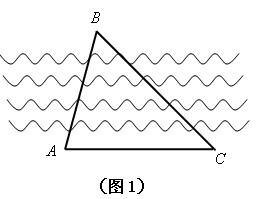
学生：思考提出测量角A，C。

教师：若已知测得

，

，如何计算A、B两地距离?

师生共同回忆解直角三角形，①直角三角形中，已知两边，可以求第三边及两个角。②直角三角形中，已知一边和一角，可以求另两边及第三个角。

教师引导：

是斜三角形，能否利用解直角三角形，精确计算AB呢?

学生：(思考交流)得出过

作

于

(如图2)，把

分为两个直角三角形，解题过程，学生阐述，教师板书。

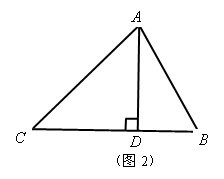
解：过

作

于

在

中，

，

在

中，

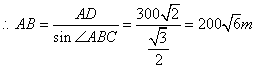
教师继续引导：在上述问题中，若

，

，能否用

、

、

表示

呢?

学生：发现

，

教师：引导  ，在刚才的推理过程中，你能想到什么?你能发现什么?

学生：发现即然有

，那么也有

，

。

教师：引导

，

，

，我们习惯写成对称形式

，

，

，因此我们可以发现

，是否任意三角形都有这种边角关系呢?

设计意图：兴趣是最好的老师。如果一节课有良好的开头，那就意味着成功的一半。因此，我通过从学生日常生活中的实际问题引入，激发学生思维，激发学生的求知欲，引导学生转化为解直角三角形的问题，在解决问题后，对特殊问题一般化，得出一个猜测性的结论——猜想，培养学生从特殊到一般思想意识，培养学生创造性思维能力。

（二）数学实验，验证猜想

教师：给学生指明一个方向，我们先通过特殊例子检验

是否成立，举出特例。

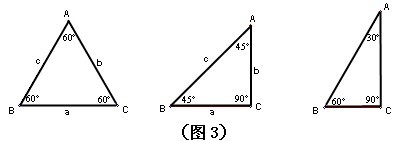
(1)在△ABC中，∠A，∠B，∠C分别为

，

，

，对应的边长a：b：c为1：1：1，对应角的正弦值分别为

，

，

，引导学生考察

，

，

的关系。(学生回答它们相等)

(2)、在△ABC中，∠A，∠B，∠C分别为

，

，

，对应的边长a：b：c为1：1：

，对应角的正弦值分别为

，

，1;(学生回答它们相等)

(3)、在△ABC中，∠A，∠B，∠C分别为

，

，

，对应的边长a：b：c为1：

：2，对应角的正弦值分别为

，

，1。(学生回答它们相等)(图3)

教师：对于

呢?

学生：思考交流得出，如图4，在Rt

ABC中，设BC=a,AC=b,AB=c,

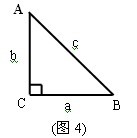
则有

，

，又

,

则

从而在直角三角形ABC中，

教师：那么任意三角形是否有

呢?

借助于电脑与多媒体，利用《几何画板》软件，演示正弦定理教学课件。边演示边引导学生观察三角形形状的变化与三个比值的变化情况。

结论：

对于任意三角形都成立。

设计意图：通过《几何画板》软件的演示，使学生对结论的认识从感性逐步上升到理性。

（三）证明猜想，得出定理

师生活动：

教师：我们虽然经历了数学实验，多媒体技术支持，对任意的三角形，如何用数学的思想方法证明

呢?前面探索过程对我们有没有启发?学生分组讨论，每组派一个代表总结。(以下证明过程，根据学生回答情况进行叙述)

学生：思考得出

(1)在

中，成立，如前面检验。

(2)在锐角三角形中，如图5设

，

，

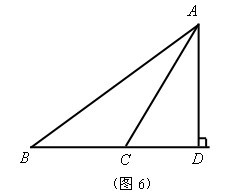
作：

，垂足为

在

中，

在

中，

同理，在

中，

(3)在钝角三角形中，如图6设

为钝角，

，

，

，作

交

的延长线于

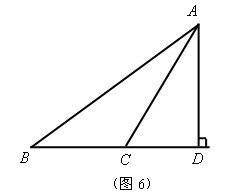
在

中，

在

中，

同锐角三角形证明可知

教师：我们把这条性质称为正弦定理：在一个三角形中，各边和它所对角的正弦的比相等，即

#FormatImgID_114#

教师：还有其它证明方法吗?

学生：思考得出，分析图形(图7)，对于任意△ABC，由初中所学过的面积公式可以得出：

，

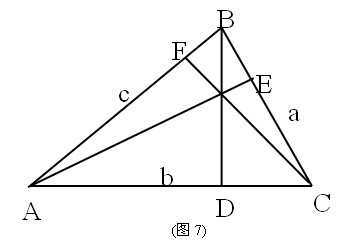
而由图中可以看出：

，

，

=

=

等式

中均除以

后可得

，

即

。

教师边分析边引导学生，同时板书证明过程。          

在刚才的证明过程中大家是否发现三角形高

，三角形的面积：

，能否得到新面积公式

学生：

得到三角形面积公式

设计意图：经历证明猜想的过程，进一步引导启发学生利用已有的数学知识论证猜想，力图让学生体验数学的学习过程。

（四）利用定理，解决引例

师生活动：

教师：现在大家再用正弦定理解决引例中提出的问题。

学生：马上得出

在

中，

（五）了解解三角形概念

设计意图：让学生了解解三角形概念，形成知识的完整性。

教师：一般地，把三角形的三个角

、

、

和它们的对边

、

、

叫做三角形的元素，已知，三角形的几个元素，求其他元素的过程叫做解三角形。

设计意图：利用正弦定理，重新解决引例，让学生体会用新的知识，新的定理，解决问题更方便，更简单，激发学生不断探索新知识的欲望。

（六）运用定理，解决例题

师生活动：

教师：引导学生从分析方程思想分析正弦定理可以解决的问题。

学生：讨论正弦定理可以解决的问题类型：

(1)如果已知三角形的任意两个角与一边，求三角形的另一角和另两边，如

;

(2)如果已知三角形任意两边与其中一边的对角，求另一边与另两角，如

。

师生：例1的处理，先让学生思考回答解题思路，教师板书，让学生思考主要是突出主体，教师板书的目的是规范解题步骤。

例1：在

中，已知

，

，

，解三角形。

分析“已知三角形中两角及一边，求其他元素”，第一步可由三角形内角和为

求出第三个角∠C，再由正弦定理求其他两边。

例2：在

中，已知

，

，

，解三角形。

例2的处理，目的是让学生掌握分类讨论的数学思想，可先让中等学生讲解解题思路，其他同学补充交流。

学生：反馈练习(教科书第5页的练习)

用实物投影仪展示学生中解题步骤规范的解答。

设计意图：自己解决问题，提高学生学习的热情和动力，使学生体验到成功的愉悦感，变“要我学”为“我要学”，“我要研究”的主动学习。

（七）尝试小结：

教师：提示引导学生总结本节课的主要内容。

学生：思考交流，归纳总结。

师生：让学生尝试小结，教师及时补充，要体现：

(1)正弦定理的内容(

)及其证明思想方法。

(2)正弦定理的应用范围：①已知三角形中两角及一边，求其他元素;②已知三角形中两边和其中一边所对的角，求其他元素。

(3)分类讨论的数学思想。

设计意图：通过学生的总结，培养学生的归纳总结能力和语言表达能力。

（八）作业设计

作业：第10页[习题1.1]A组第1、2题。

精品学习网的编辑为大家带来的高中高一数学必修5教学设计，希望能为大家提供帮助。