国考经验之数学运算及解题思路的七大方法（上）

一.排列组合问题

1.    能不用排列组合尽量不用。用分步分类，避免错误

2.    分类处理方法，排除法。

例：要从三男两女中安排两人周日值班，至少有一名女职员参加，有(C1/2 *C1/3 +1)种不同的排法?

析：当只有一名女职员参加时，C1/2* C1/3;

当有两名女职员参加时，有1种

 

3．特殊位置先排

例：某单位安排五位工作人员在星期一至星期五值班，每人一天且不重复。若甲忆两人都不能安排星期五值班，则不同的排班方法共有(3 * P4/4)

析：先安排星期五，后其它。

 

4. 相同元素的分配（如名额等，每个组至少一个），隔板法。

例：把12个小球放到编号不同的8个盒子里，每个盒子里至少有一个小球，共有(C7/11)种方法。

析：0 0 0 0 0 0 0 0 0 0 0 0 ，共有12-1个空，用8-1个隔板插入，一种插板方法对应一种分配方案，共有C7/11种，即所求。

注意：如果小球也有编号，则不能用隔板法。

 

5. 相离问题（互不相邻）用插空法

　例：7人排成一排，甲、乙、丙3人互不相邻，有多少种排法?

析：| 0 | 0 | 0 | 0 |,分两步。第一步，排其它四个人的位置，四个0代表其它四个人的位置，有P4/4种。第二步，甲乙丙只能分别出现在不同的 | 上，有P3/5种，则P4/4 * P3/5即所求。

例：在一张节目表中原有8个节目，若保持原有的相对顺序不变，再增加三个节目，求共有多少种安排方法?

析：

思路一，用二次插空法。先放置8个节目，有9个空位，先插一个节目有9种方法，现在有10个空位，再插一个节目有10种方法，现有11种空位，再插一种为11种方法。则共有方法9*10*11。

思路二，可以这么考虑，在11个节目中把三个节目排定后，剩下的8个位置就不用排了，因为8个位置是固定的。因此共有方法P3/11

6. 相邻问题用捆绑法

例：7人排成一排，甲、乙、丙3人必须相邻，有多少种排法?

析：把甲、乙、丙看作整体X。第一步，其它四个元素和X元素组成的数列，排列有P5/5种;第二步，再排X元素，有P3/3种。则排法是P5/5 * P3/3种。

7. 定序问题用除法

例：有1、2、3，...，9九个数字，可组成多少个没有重复数字，且百位数字大于十位数字，十位数字大于个位数字的5位数?

析：

思路一：1-9，组成5位数有P5/9。假设后三位元素是(A和B和C，不分次序，ABC任取)时(其中B>C>A),则这三位是排定的。假设B、C、A这个顺序，五位数有X种排法，那么其它的P3/3-1个顺序，都有X种排法。则X*(P3/3-1+1)=P5/9,即X=P5/9 / P3/3 

思路二：分步。第一步，选前两位，有P2/9种可能性。第二步，选后三位。因为后三位只要数字选定，就只有一种排序，选定方式有C3/7种。即后三位有C3/7种可能性。则答案为P2/9 * C3/7

 

8. 平均分组

例：有6本不同的书，分给甲、乙、丙三人，每人两本。有多少种不同的分法?

析：分三步，先从6本书中取2本给一个人，再从剩下的4本中取2本给另一个人，剩下的2本给最后一人，共C2/6* C2/4 * C2/2

例：有6本不同的书，分成三份，每份两本。有多少种不同的分法?

析：分成三份，不区分顺序，是无序的，即方案(AB,CD,EF)和方案(AB,EF,CD)等是一样的。前面的在(C2/6* C2/4 * C2/2)个方案中，每一种分法，其重复的次数有P3/3种。则分法有，(C2/6* C2/4 * C2/2) /   P3/3 种分法。

二.日期问题

1.闰年，2月是29天。平年，28天。

2.口诀：

平年加1，闰年加2;(由平年365天/7=52余1得出)。

例：2002年 9月1号是星期日  2008年9月1号是星期几?

因为从2002到2008一共有6年，其中有4个平年，2个闰年，求星期，则：

4X1+2X2=8，此即在星期日的基础上加8，即加1，第二天。

 

例：2004年2月28日是星期六,那么2008年2月28日是星期几?

4+1=5，即是过5天，为星期四。(08年2 月29日没到)

三.集合问题

1.两交集通解公式（有两项）

公式为：满足条件一的个数+满足条件二的个数-两者都满足的个数=总个数-两者都不满足的个数

其中满足条件一的个数是指 只满足条件一不满足条件二的个数 加上 两条件都满足的个数  公式可以画图得出

例：有62名学生，会击剑的有11人，会游泳的有56人，两种都不会用的有4人，问两种都会的学生有多少人?

思路一：两种都会+只会击剑不会游泳+只会游泳不会击剑=62-4

设都会的为T，11-T+56-T+T=58，求得T=9

思路二：套公式，11+56-T=62-4，求得T=9

例：对某小区432户居民调查汽车与摩托车的拥有情况，其中有汽车的共27户，有摩托车的共108户，两种都没有的共305户，那么既有汽车又有摩托车的有多少户?

析：套用公式27+108-T=432-305 得T=8

 

2.三交集公式（有三项）

　例：学校教导处对100名同学进行调查，结果有58人喜欢看球赛，有38人喜欢看戏剧，有52人喜欢看电影。另外还知道，既喜欢看球赛又喜欢看戏剧(但不喜欢看电影)的有6人，既喜欢看电影又喜欢看戏剧(但不喜欢看球赛)的有4人，三种都喜欢的有12人，则只喜欢看电影的人有多少人?

#FormatImgID_0#

如图， U=喜欢球赛的 + 喜欢戏剧的 + 喜欢电影的

X表示只喜欢球赛的人; Y表示只喜欢电影的人; Z表示只喜欢戏剧的人

T是三者都喜欢的人。即阴影部分。

a表示喜欢球赛和电影的人。仅此2项。不喜欢戏剧

b表示喜欢电影和戏剧的人。仅此2项。不喜欢球赛

c表示喜欢球赛和戏剧的人。仅此2项。不喜欢电影。

A=X+Y+Z,B=a+b+c,A是只喜欢一项的人，B是只喜欢两项的人，T是喜欢三项的人。

则U=喜欢球赛的 + 喜欢戏剧的 + 喜欢电影的 = (x+a+c+T) + (y+a+b+T) + (z+b+c+T)

整理，即

A+2B+3T=至少喜欢一项的人数人

又：A+B+T=人数

再B+3T= 至少喜欢2项的人数和

则

原题解如下：

A+2*(6+4+c)+3*12=58+38+52

A+(6+4+c)+12=100

求得c=14

则只喜欢看电影的人=喜欢看电影的人数-只喜欢看电影又喜欢球赛的人-只喜欢看电影又喜欢看戏剧的人-三者都喜欢的人=52-14-4-12=22人 

 

四.时钟问题

1.时针与分针

分针每分钟走1格，时针每60分钟5格，则时针每分钟走1/12格，每分钟时针比分针少走11/12格。

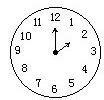
例：现在是2点，什么时候时针与分针第一次重合?

析：2点时候，时针处在第10格位置，分针处于第0格，相差10格，则需经过10 /  11/12 分钟的时间。

例：中午12点，时针与分针完全重合，那么到下次12点时，时针与分针重合多少次?

析：时针与分针重合后再追随上，只可能分针追及了60格，则分针追赶时针一次，耗时60 / 11/12 =720/11分钟，而12小时能追随及12*60分钟/ 720/11 分钟/次=11次，第11次时，时针与分针又完全重合在12点。如果不算中午12点第一次重合的次数，应为11次。如果题目是到下次12点之前，重合几次，应为11-1次，因为不算最后一次重合的次数。

 

2.分针与秒针

秒针每秒钟走一格，分针每60秒钟走一格，则分针每秒钟走1/60格，每秒钟秒针比分针多走59/60格

例：中午12点，秒针与分针完全重合，那么到下午1点时，两针重合多少次?

析：秒针与分针重合，秒针走比分针快，重合后再追上，只可能秒针追赶了60格，则秒针追分针一次耗时，60格/ 59/60格/秒= 3600/59秒。而到1点时，总共有时间3600秒，则能追赶，3600秒 / 3600/59秒/次=59次。第59次时，共追赶了，59次*3600/59秒/次=3600秒，分针走了60格，即经过1小时后，两针又重合在12点。则重合了59次。

 

3.时针与秒针

时针每秒走一格，时针3600秒走5格，则时针每秒走1/720格，每秒钟秒针比时针多走719/720格。

例：中午12点，秒针与时针完全重合，那么到下次12点时，时针与秒针重合了多少次?

析：重合后再追上，只可能是秒针追赶了时针60格，每秒钟追719/720格，则要一次要追60 / 719/720=43200/719 秒。而12个小时有12*3600秒时间，则可以追12*3600/43200/719=710次。此时重合在12点位置上，即重合了719次。

 

4.成角度问题

例：在时钟盘面上，1点45分时的时针与分针之间的夹角是多少?

析：一点时，时针分针差5格，到45分时，分针比时针多走了11/12*45=41.25格，则分针此时在时针的右边36.25格，一格是360/60=6度，则成夹角是,36.25*6=217.5度。

 

5.相遇问题

例：3点过多少分时，时针和分针离“3”的距离相等，并且在“3”的两边?

析：作图，此题转化为时针以每分1/12速度的速度，分针以每分1格的速度相向而行，当时针和分针离3距离相等，两针相遇，行程15格，则耗时15 / (1+ 1/12 )=180/13分。

例：小明做作业的时间不足1时，他发现结束时手表上时针、分针的位置正好与开始时时针、分针的位置交换了一下。小明做作业用了多少时间?

析：

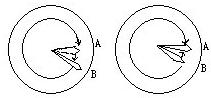
只可能是这个图形的情形，则分针走了大弧B-A，时针走了小弧A-B，即这段时间时针和分针共走了60格，而时针每分钟1/12格，分针1格，则总共走了60/ (1/12+1)=720/13分钟，即花了720/13分钟。

五.方阵问题

1、方阵外一层总人数比内一层的总人数多8

2、每边人数与该层人数关系是：最外层总人数＝（边人数－1）×4

3、方阵总人数＝最外层每边人数的平方

4、空心方阵的总人(或物)数=（最外层每边人(或物)数－空心方阵的层数）×空心方阵的层数×4

5、去掉一行、一列的总人数=去掉的每边人数*2-1

例：某校的学生刚好排成一个方阵，最外层的人数是96人，问这个学校共有学生?

析：最外层每边的人数是96/4+1=25，刚共有学生25*25=625

例：五年级学生分成两队参加学校广播操比赛，他们排成甲乙两个方阵，其中甲方阵每边的人数等于8，如果两队合并，可以另排成一个空心的丙方阵，丙方阵每边的人数比乙方阵每边的人数多4人，甲方阵的人数正好填满丙方阵的空心。五年级参加广播操比赛的一共有多少人?

析：

设乙最外边每人数为Y，则丙为Y+4.

8*8+Y*Y+8*8=(Y+4)(Y+4)

求出Y=14,则共有人数：14*14+8*8=260

例：明明用围棋子摆成一个三层空心方阵，如果最外层每边有围棋子15个，明明摆这个方阵最里层一周共有多少棋子?摆这个三层空心方阵共用了多少个棋子?

析：

最外层有(15-1)*4=56个。则里二层为56-8*2=40

应用公式，用棋子(15-3)*3*4=144

六.几何问题

1.公式

#FormatImgID_4#

#FormatImgID_5#

补：扇形面积=1/2*r*l    其中r为半径，l为弧长。

 

2.两三角形，有一角成互补角，或者有一角重合的面积关系。

#FormatImgID_6#

图1中，Sabc / Scde=BC/CE * AC/CD

图2中，Sabc / Sade=AB/AD * AC/AE (皆可通过作高，相似得到)

例： 如图，三角形ABC的面积为1，并且AE=3AB，BD=2BC，那么△BDE的面积是多少？

#FormatImgID_7#

Sbde=Sabc * BE/AB * BD/BC =1 * 2 * 2 =4  例：　例4 如下图，将凸四边形ABCD的各边都延长一倍至 A′、B′、 C′、D′，连接这些点得到一个新的四边形A′B′C′D′，若四边形A′B′C′D′的面积为30平方厘米，那么四边形ABCD的面积是多少?

#FormatImgID_8#

Sa’ad’+Sb’cc’=2*Sabcd

同理Sa’b’b+Sdc’d’=2Sabcd

则Sabcd=30/(2+2+1)=6

3.圆分割平面公式

公式为：N^2-N+2,其中N为圆的个数。

一个圆能把平面分成两个区域，两个圆能把平面分成四个区域，问四个圆能最多把平面分成多少个区域?(4^2-4+2 )

4.最大和最小

（1）等面积的所有平面图形当中，越接近圆的图形，其周长越小。

（2）等周长的所有平面图形当中，越接近圆的图形，其面积越大。

以上两条定理是等价的。

（3）等体积的所有空间图形当中，越接近球体的几何体，其表面积越小。

（4）等表面积的所有空间图形当中，越接近球体的几何体，其体积越大。

以上两条定理是等价的。

例：相同表面积的四面体,六面体,正十二面体及正二十面体,其中体积最大的是:

A 四面体  B 六面体  C 正十二面体  D 正二十面体

析：显然，正二十面体最接近球体，则体积最大。

5.一个长方体形状的盒子长、宽、高分别为20厘米、8厘米和2厘米，现在要用一张纸将其六个面完全包裹起来，要求从纸上剪下的部分不得用作贴补，请问这张纸的大小可能是下列哪一个?（    ）

A.长25厘米、宽17厘米            B.长26厘米、宽14厘米

C.长24厘米、宽21厘米            D.长24厘米、宽14厘米

析：这种题型首先的思路应该是，先算盒子的总面积=2*(20*8+20*2+8*2)=432，除了C其它都小于432。

 

七.比例问题、十字相乘法与浓度问题

1.十字相乘法

一个集合中的个体，只有2个不同的取值，部分个体取值为A，剩余部分取值为B。平均值为C。求取值为A的个体与取值为B的个体的比例。假设A有X，B有(1-X)。则C为1。

得式子，A*X+B*(1-X)=C*1

整理得X=C-B / A-B   1-X=A-C / A-B

则有X : (1-X)=C-B / A-C

计算过程写为

X        A          C-B

：= C

1-X      B          A-C         (一般大的写上面A, 小的B。)

例：某体育训练中心，教练员中男占90%，运动员中男占80%，在教练员和运动员中男占82%，教练员与运动员人数之比是

析：一个集合(教练员和运动员的男性)，只有2个不同的取值，部分个体取值(90%),剩余部分取值为82%，平均值为82%。

教练员   90%         2%

82%= 1:4

运动员   80%         8%

例：某班男生比女生人数多80%，一次考试后，全班平均成级为75 分，而女生的平均分比男生的平均分高20% ，则此班女生的平均分是：

析：男生平均分X，女生1.2X

1.2X         75-X        1

75            =

X           1.2X-75     1.8

得X=70 女生为84

 

2.浓度问题

溶液的重量＝溶质的重量+溶剂的重量

浓度＝溶质的质量 / 溶液质量

浓度又称为溶质的质量分数。

关于稀释，加浓，配制。其中混合后的浓度为P.

稀释，一溶液加水，相当于a克P1%的溶液，和b克0%的溶液配制。

P1           P        a

P

0            P1-P      b

加浓，相当于a克p1%的溶液，和b克100%的溶液配制。

P1          P-100    a

P

100         P1-P     b

配制则是a克P1%的溶液，和b克P2%的溶液配制。

可列以下十字相乘：

P1        P-P2      a

P

P2        P1-P      b

注：有些题不用十字相乘法更简单。

例：有含盐15%的盐水20千克，要使盐水含盐20%,需加盐多少千克?

析：

15            80       20

20

100           5        b

80/5=20/b 得b=1.25g

例：从装满100g浓度为80%的盐水杯中倒出40g盐水后再倒入清水将杯倒满，这样反复三次后，杯中盐水的浓度是()

A.17.28%    B.28.8%      C.11.52%    D.48%

析：开始时，溶质为80克。第一次倒出40g，再加清水倒满，倒出了盐80*40%，此时还剩盐80*60%。同理，第二次，剩80*60%*60%。第三次，乘80*60%^3=17.28g，即浓度为17.28%

特例：

有甲乙两杯含盐率不同的盐水，甲杯盐水重120克，乙杯盐水重80克.现在从两杯倒出等量的盐水，分别交换倒入两杯中.这样两杯新盐水的含盐率相同.从每杯中倒出的盐水是多少克?

析：设甲浓度P1,乙浓度P2。混合后的相等浓度为P.拿出的等量的水为a

则对于甲  P1       P-P2      120-a       P  P2       P1-P      a

对于乙 P2         P-P1      80-a      P

P1         P2-P      a

则120-a       a  :       =      :  a             80-a

得a=120*80 / 120+80

一般地，对于质量为m1,m2的溶液，也有a=m1*m2  /  (m1+m2)

国考经验之数学运算及解题思路的七大方法（上）

相关推荐：

更多公务员经验心得（点击进入）