对于广大备考的考生来讲，如何能够找到跟考试内容贴近的最新的辅导资料是大家最为关心的问题，精品学习网为您提供了2015年国考行测数量关系最值问题，希望对于您的复习备考起到巨大的作用!

【例题】草地上插了若干根旗杆，已知旗杆的高度在1至5米之间，且任意两根旗杆的距离都不超过它们高度差的10倍。如果用一根绳子将所有旗杆都围进去，在不知旗杆数量和位置的情况下，最少需要准备多少米长的绳子?( )

A. 40 B. 100

C. 60 D. 80

题目中问至少准备多少米的绳子，那么咱们考虑问题时候是找到用绳子最多的情况还是用绳子最少的情况呢?如果我们仔细考虑发现这两种情况都不对。用绳子最少的情况是这种极限，所有的旗杆都插在一个点上，那么所需要的绳子为0米。用绳子最多的情况也可以是这样，在某种旗杆的分布情况下，我们不必把绳子拉紧环绕，而是松松垮垮围在周围，那么想用多少米就可以是多少米。

题干问题是“最少需要准备多少米长的绳子”，假设是某个人需要准备多少米长的绳子。这个人知道“旗杆的高度在1至5米之间，且任意两根旗杆的距离都不超过它们高度差的10倍”这个规律，但是对于旗杆是怎么分布的是不知道也是不能控制的。这个人可以控制绳子的围绕形式，或者是松松垮垮的围绕或者是拉紧的环绕。他的目的是想让绳子用得最少，那么对于他可以控制的，比如绳子是否拉紧环绕，他就采取绳子最少的形式，也就是拉紧环绕。而对于他控制不了的情况——旗杆的分布，他是无能为力的。

现在不能控制的因素是旗杆的分布，旗杆分布导致绳子所用的多或者少。他必须保证绳子可以围住旗杆，那么他带的绳子可以围住用绳子最多情况的旗杆分布，那么其他情况下旗杆的分布也就可以满足被围住。那么我们所找的情况就是在绳子紧绷围住情况使用绳子最多的旗杆分布情况。

旗杆数是无限的，现在我们先分析两个旗杆(假设是1米和5米)情况，两根旗杆应该采用最大距离，才能用绳子最多。

如果是三个旗杆，我们假设新加入一个2米的旗杆，或者这个两米旗杆在一米和五米旗杆之间线段上，或者在两个旗杆线段之外，如下图。

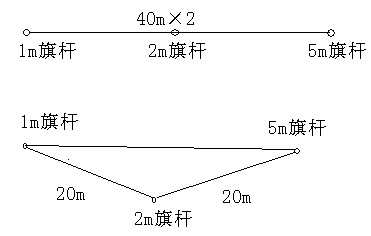
如果2m旗杆不在1m和5m旗杆的连线上，并且使2m旗杆与1m和5m旗杆都达到最大距离20米，那么根据三角形任意两边大于第三边，1m旗杆与5m旗杆之间的距离要小于40m，那么所用绳子小于80m。所以要使所用绳子最多，则需要三个旗杆在一条直线上。

四个旗杆的情况可以在三个旗杆的基础上继续考虑，只是更加复杂，分析情况更多，但是所得结论仍是在同一条直线上所用的绳子最多。

ps：本站稿件未经许可不得转载，转载请保留出处及原文地址。

以上就是精品学习网为您提供的2015年国考行测数量关系最值问题，不知道是否是您想要的辅导资料，更多尽在精品学习网~