行测数量关系解题方法：公式巧解边端计数

边端计数问题是与我们日常生活联系非常紧密的一类问题。本质上，边端计数问题研究的“段”与“段点”之间关系关系。具体来说，主要有两种题型：植树问题和方阵问题。下面华图教育研究员将通过具体例题来给大家做详细的解释。

一、植树问题

单边线型植树公式：棵数=总长÷间隔+1;总长=(棵数-1)×间隔

单边环型植树公式：棵数=总长÷间隔;总长= 棵数×间隔

单边楼间植树(锯木、爬楼)公式：棵数=总长÷间隔-1;总长=(棵数+1)×间隔

注意：只要是直线型的路，不管有没有转弯，只要没有封闭就可以认为是线型植树问题;只要是封闭式的路，不管是什么形状的，我们都可以认为是环型植树问题。如果是双边植树，就在单边的基础上直接乘以2就可以了。

二、方阵问题

N阶实心方阵：总人数=

=(外圈人数÷4+1)2 ;最外圈为4N-4人;相邻两圈相差8人。

注意：给出的公式都是实心方阵适用的，也就是这类方阵中间是4人，如果题中给出的是中空方阵，那么就是意味着方阵的中间不是4人，因此在审题的时候大家务必要细心。

【例1】某单位购买一批树苗计划在一段路两旁植树。若每隔5米种1棵树，可以覆盖整个路段，但这批树苗剩20棵。若每隔4米种1棵树且路尾最后两棵树之间的距离为3米，则这批树苗刚好可覆盖整个路段。这段路长为( )。

A.395米B.205米

C.375米D.195米

【答案】D

【解析】这道题是边端计数问题中的双边线性植树问题，解题的关键点在于注意是两旁也就是双边植树，还有就是处理好“若每隔4个种1棵树且路尾最后两棵树之间的距离为3米，则这批树苗刚好可覆盖整个路段”这样的不适合公式的形式。这里我们可以设这段路长

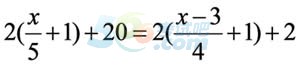
是x米，那么可列方程可以解出x=195，选择D选项。

【例2】一根绳子对折三次后，从中剪断，共剪成( )段绳子。

A.9B.6

C.5D.3

【答案】A

【解析】本题是边端计数问题中的剪绳问题，从中间剪断只需要简一刀即可，套用公式，23×1+1=9，选择A选项。

【例3】某学校举行运动会，学生排成一个方阵，最外层的人数是80人，问这个方阵共有学生多少人?( )

A.361人B.406人

C.441人D.486人

【答案】C

【解析】本题是边端计数问题中的方阵问题，既然是方阵，总人数一定是个平方数，我们可以首先排除B、D选项。我们可以直接套用公式计算得出总人数是(80÷4+1)2=212=441,选择C选项。

通过以上几道例题的解析，大家会发现边端计数问题主要是对公式的考察，只要大家把相应的公式记牢，这部分的题目还是很容易把握的。但是在记公式的同时还要对应好题型，这样的复习才更有效

行测数量关系解题方法：公式巧解边端计数