组合数学是一个既古老又年轻的数学分支。说它古老,因为它所研究的问题有的可追溯到很久很久以前。然而,它形成一个新的分支还是最近若干年的事,是受到电子计算机蓬勃发展影响的结果。?

本节中的排列与组合、容斥原理、抽屉原理都是组合数学的内容。?

组合数学研究的主要内容是计数和枚举，即计算具有某种特性的对象有多少,并进而把它完全列举出来。“计数”在许多方面有其重大作用,比如本节中的概率部分，就是计数的应用——要计算发生具有某种性质的事件的概率,往往首先要计算出具有该性质的事件的数目。?

◎排列与组合

加法原理与乘法原理是在计数研究中最常用也是最基本的两个法则。?

一、加法原理?

完成一件事有两类不同方案(其中的方法互不相同)。在第1类方案中有?m种不同的方法，在第2类方案中有n种不同的方法，那么完成这件事共有m+n种不同的方法。??

例如：小华正准备出国留学，不是去A国，就是去B国。其中A国有4所大学向他发出了录取通知，而B国则有5所大学向他发出了入学邀请。故小华共有9所大学可以选择，即共有9种留学方案。?

二、乘法原理?

完成一件事需要两个步骤(第1步方法的选取不会影响第2步方法的选取)。做第1步有?m种不同的方法，做第2步有n种不同的方法，那么完成这件事共有m×n种不同的方法。??

例如，从A到B有3条不同的道路,从B到C有2条不同的道路,则从A经B到C的道路数n=3×2=6。

三、排列与组合?

排列组合的难点主要体现在对排列组合原理的理解与运用上，也即确定是排列还是组合。排列与组合，前者与顺序有关，后者与顺序无关。考生可以通过任选一种安排好的情况，调整其中两个物体的前后顺序，看是否会出现新的情形，若是则与顺序有关，反之则与顺序无关。对基本的排列组合题能够迅速判断是排列还是组合，并写出对应方法数。考生可通过多考虑一些应用环境来锻炼自己判断排列组合的能力。?

排列公式：?

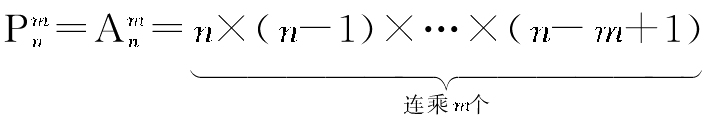
组合公式：

◎容斥原理

容斥原理又称包含排斥原理，它是解决组合计数问题的重要工具。?

加法原理告诉我们，在集合间没有交集的情况下，求这些集合并集的简单计数公式。容斥原理则告诉我们一般情况下的公式，此时集合间可以重叠而没有限制。?

例如，在1到30的正整数中，有多少个整数能被2整除或能被3整除??

由于从1开始每连续2个的第2个数能被2整除，所以1到30中能被2整除的整数共30÷2=15个，它们分别是?

2,4,6,8,10,12,14,16,18,20,22，24,26,28,30。?

同理，由于从1开始每连续3个的第3个数能被3整除，所以1到30中能被3整除的整数共30÷3=10个，它们分别是?

3,6,9,12,15,18,21,24,27,30。?

又，同时能被2和3整除的整数共30÷(2×3)=5个，分别是?

6,12,18,24,30。?

所以计数时如果计算15+10=25，则重复计算了5个数。容斥原理可以帮我们巧妙地解决这一问题。?

|A∪B|=|A|+|B|-|A∩B|?

|A∪B∪C|=|A|+|B|+|C|-|A∩B|-|B∩C|-|C∩A|+|A∩B∩C|?

其中，两集合容斥原理用简单语言叙述就是：?

满足条件1的个数+满足条件2的个数-都满足的个数=总数-都不满足的个数=满足至少一个条件的个数。?

◎抽屉原理

抽屉原理是组合数学里最简单也是最基本的原理：?n+1个物品放入n个抽屉中，则至少有一个抽屉，其中有两个或更多的物品。也有人称之为“鸽巢原理”,即“若有n个鸽子巢,n+1只鸽子,则至少有一个鸽子巢里至少有两只鸽子”。??

从这样一个看来是显而易见的原理出发,可以导出许多组合数学中的并不那么显而易见的有趣结论。下面先举几个例子,通过例子说明利用抽屉原理的一般步骤,从不同的例题中总结出规律。?

例：?

抽屉里有10双手套,从中取11只出来,其中至少有两只是完整配对的。?

某次会议有?n位代表参加,每一位代表至少认识其余n-1位中的一位,则n位代表中,至少有两位认识的人数相等。??

公考中，抽屉原理题目表述多为“黑色布袋中有……(具体物品)，至少要取出多少个，才可以保?证……?(满足目标)”。?

解决方案为反向构造。即假设所有物品并非放在布袋中，而是在自己手中，然后逐一发出，在发出的过程中尽可能不要满足题目的目标，直到满足目标为止。那么在尽量不满足题目要求情况下发出的最多数目就是题目的答案。

◎概率

概率论是研究随机现象的学科。概率问题是公务员考试最近几年开始考查的问题，主要有古典概型、几何概型以及条件概率。?

一、古典概型?

古典概型，又称等可能概型。古典概型的特点：?

(1)试验中所有可能出现的基本事件只有有限个。?

(2)每个基本事件出现的可能性相等。?

古典概型：?

二、几何概型

如果每个事件发生的概率只与构成该事件区域的长度(面积或体积)成比例，则称为几何概型。?

几何概型的特点：?

(1)试验中所有可能出现的基本事件有无限多个。?

(2)每个基本事件出现的可能性相等。?

几何概型：?

三、条件概率?

条件概率是指事件A已发生的条件下事件B发生的概率。?

例如，将一枚硬币抛掷两次，观察其出现正反面的情况。设事件A为“至少有一次为正面”，事件B为“两次掷出同一面”。现求已知事件A已经发生的条件下事件B发生的概率。?