一般来说，考试中常考的集合关系主要有下面两种：

1. 并集∪ 定义：取一个集合，设全集为I，A、B 是I 中的两个子集，由所有属于A 或

属于B 的元素所组成的集合，叫做A，B 的并集，表示：A∪B。

比如说，现在要挑选一批人去参加篮球比赛。条件A 是，这些人年龄要在18 岁以上，

条件B 是，这些人身高要在180CM 以上， 那么符合条件的人就是取条件A 和B 的并集，就是

两个条件都符合的人：18 岁以上且身高在180CM 以上。

2. 交集∩ 定义：(交就是取两个集合共同的元素)A 和B 的交集是含有所有既属于A

又属于B 的元素，而没有其他元素的集合。A 和B 的交集写作“A∩B”。形式上：x 属于A∩B

当且仅当x 属于A 且x 属于B。

例如：集合{1，2，3}和{2，3，4} 的交集为{2，3}。数字9 不属于素数集合{2，3，5，

7，11} 和奇数集合{1，3，5，7，9，11｝的交集。若两个集合A 和B 的交集为空，就是说他

们没有公共元素，则他们不相交。

(I)取一个集合，设全集为I，A、B 是I 中的两个子集，X 为A 和B 的相交部分，则集

合间有如下关系：

A∩B=X，A+B=A∪B-X;文氏图如下图。

下面让我们回顾一下历年国考和地方真题，了解一下文氏图的一些应用。

例：如下图所示，X、Y、Z 分别是面积为64、180、160 的三个不同形状的纸片，它们

部分重叠放在一起盖在桌面上，总共盖住的面积为290，且X 与Y、Y 与Z、Z 与X 重叠部分面

积分别为24、70、36，问阴影部分的面积是多少?( )

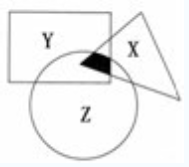
A. 15 B. 16

C. 14 D. 18

【答案：B】从题干及提供的图我们可以看出，所求的阴影部分的面积即(II)中的x，直

接套用上述公式，我们可以得到：X∪Y∪Z=64+180+160，X∩Z=24，X∩Y=36，Y∩Z=70，

则：x=X∪Y∪Z-[X+Y+Z-X∩Z-X∩Y-Y∩Z]=290-[64+180+160-24-70-36]=16

从图上可以清楚的看到，所求的阴影部分是X，Y，Z 这三个图形的公共部分。即图1 中的x，由题意有：64+180+160-24-70-36+x=290，解得x=16。

例：旅行社对120 人的调查显示，喜欢爬山的与不喜欢爬山的人数比为5：3，喜欢游泳

的与不喜欢游泳的人数比为7：5，两种活动都喜欢的有43 人，对这两种活动都不喜欢的人数是( )。

A. 18 B. 27 C. 28 D. 32

【答案：A】欲求两种活动都喜欢的人数，我们可以先求出两种活动都不喜欢的人数。套

用(I)中的公式：喜欢爬山的人数为120×58 =75，可令A=75;喜欢游泳的人数为120×712

=70，可令B=70;两种活动都喜欢的有43 人，即A∩B=43，故两项活动至少喜欢一个的人数

为75+70-43=102 人，即A∪B=105，则两种活动都不喜欢的人数为120-102=18(人)。

例：某外语班的30 名学生中，有8 人学习英语，12 人学习日语，3 人既学英语也学日

语，问有多少人既不学英语又没学日语?( )

A. 12 B. 13 C. 14 D. 15

【答案：B】题中要求的是既不学英语又不学日语的人数，我们可以先求出既学英语又学

日语的人数。总人数减去既学英语又学日语的人数即为所求的人数。套用上面的公式可知，即学

英语也学日语的人数为8+12-3=17，则既不学英语又没学日语的人数是：30-(8+12-3)=13。

例：电视台向100 人调查昨天收看电视情况，有62 人看过2 频道，34 人看过8 频道，

11 人两个频道都看过。问，两个频道都没有看过的有多少人?( )

A.4 B.15 C.17 D.28

答案：B】本题解法同上，直接套用上述公式求出既看过2 频道又看过8 频道的人数为62+34-11=85 人，则两个频道都没看过的有100-85=15 人。