行测指导数量关系之立体几何问题
编辑:sx_liss
2014-10-28
行测指导数量关系之立体几何问题
一、 球、圆柱与锥体
平面图形通常要计算周长、面积,对立体图形则计算表面积、体积。

二、正多面体
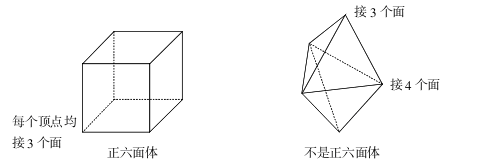
正多面体指各面都是全等的正多边形且每个顶点所接面数都是一样的凸多面体。这个定义有两个要点①每个面全等;②顶点所接面数均相等。如正方体每个面都是全等的正方形;每个顶点都接3个面,所以它是正六面体。
在《几何原本》3 的最后一卷(第13卷)中,欧几里得给出了五个正多面体的做法,并且证明只存在这五个正多面体。它们是:
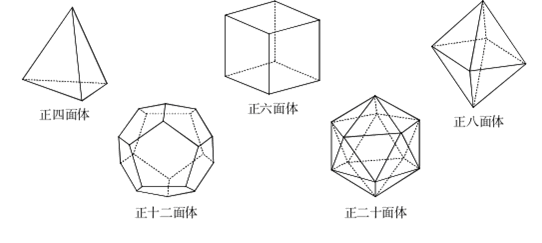
考生需要着重掌握前三个正多面体,因为这三个正多面体易于计算与想象,真题多有涉及。
【例题2】 连接正方体每个面的中心构成一个正八面体(如下图所示)。已知正方体的边长为6厘米,问正八面体的体积为多少立方厘米?
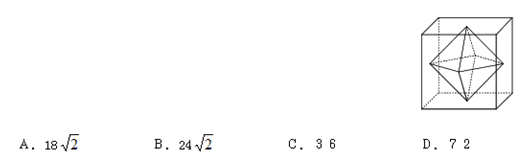
解析:此题的一般思路是在脑海中搜寻正八面体的体积计算公式,而这个公式我们不常用。
从方法优化来看,解决复杂体积问题的核心是将其转化为简单几何体进行计算。
由图不难看出,正八面体可以看成由上下(或左右)两个椎体(是正四面体)组成。锥体的高等于正方体棱长的一半,为3;锥体的底面是正方体四面中心的连线,面积等于正方

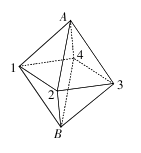
【例题3】 一个正八面体两个相对的顶点分别为A和B,一个点从A出发,沿八面体的棱移动到B位置,其中任何顶点最多到达1次,且全程必须走过所有8个面的至少1条边,问有多少种不同的走法?( )
A.8 B.16 C.24 D.32
解析:如图所示,把这个正八面体的各顶点标记。从A点出发沿棱移动到达B点。任何顶点最多到达1次,说明A和B分别是起点和终点,且中途不能经过。从A点到1点后只能有两种路径满足经过所有8个面即A-1-2-3-4-B或A-1-4-3-2-B。依此类推,从A到B有2×4=8种走法。
行测指导数量关系之立体几何问题
标签:数量关系
免责声明
精品学习网(51edu.com)在建设过程中引用了互联网上的一些信息资源并对有明确来源的信息注明了出处,版权归原作者及原网站所有,如果您对本站信息资源版权的归属问题存有异议,请您致信qinquan#51edu.com(将#换成@),我们会立即做出答复并及时解决。如果您认为本站有侵犯您权益的行为,请通知我们,我们一定根据实际情况及时处理。