学习奥数主要是锻炼我们的数学思维以及对右脑的开发都有一定的好处，下面为大家分享奥数计数问题之标数法经典例题讲解，欢迎大家参考学习！

例1、一只蜜蜂从A处出发，回到家里B处，每次只能从一个蜂房爬向右侧邻近的蜂房而不准逆行，共有多少种回家的方法?

解答：蜜蜂“每次只能从一个蜂房爬向右侧邻近的蜂房而不准逆行”这意味着它只能从小号码的蜂房爬进相邻的大号码的蜂房。明确了行走路径的方向，就可运用标数法进行计算。

如图所示，小蜜蜂从A出发到B处共有89种不同的回家方法。

例2、按图中箭头所指的方向行走，从A到I共有多少条不同的路线?

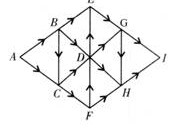
解答：

第1步：在起点A处标1。再观察点B，要想到达点B，只有一个入口A，所以在B点也标1。

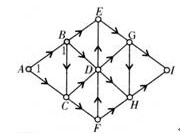
第2步：再观察点C，要想到达点C,它有两个入口A和B，所以在点C处标1+1=2。

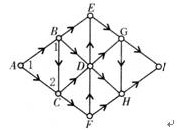
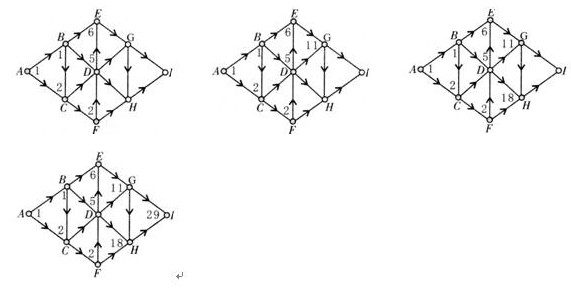
同理重复点F，点D，点E，点G，点H，点I

例3、 有一个5位数,每个数字都是1,2,3,4,5中的一个,并且相临两位数之差是1.那么这样的5位数到底有多少个呢?(数字可以重复)

这是一道数论的题目,但是我们也可以使用标数法来解答,并且非常直观.

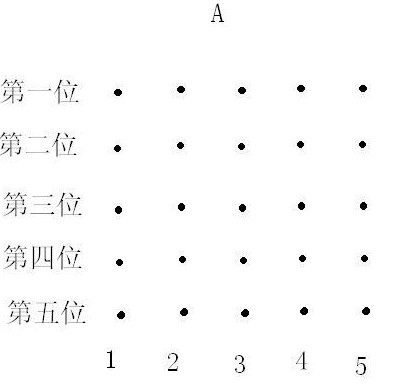
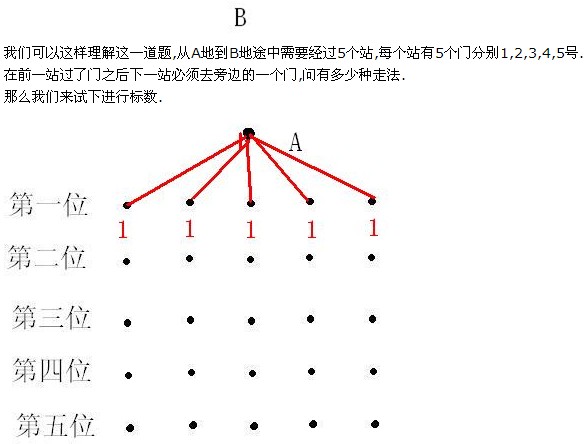
到第一站可以有5种选择,每种选择有一种走法,

那么下一站,

走1号门就只有一种走法(就是第一站走的2号门),

走2号门就有2种走法(第一站走1号或3号门)

走3号门也是2种走法(第一站走2号门或4号门)

走4号门2种走法(第一站走3号门或者5号门)

走5号门只有一种走法(第一站走的是4号门)

我们发现在这一站经过某个门有多少种走法,正好等于他左上和右上的两个数字和.于是我们可以将数字标全.

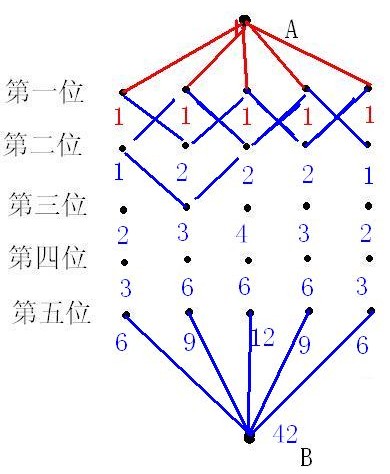
这道题的答案就是42种,

虽然很多同学会用枚举法也能做出42种,但是一旦这道题给的不是5位数,而是7位数,9位数的话,枚举法就显得无力了.这种时候标数法是个不错的选择.

可以用到标数法的问题有很多，大家掌握这种方法之后可以解决很多平时看起来很麻烦的题目。

例4、某城市的街道非常整齐(如图),从西南角A处走到东北角B处,要求走得最近的路,并且不能通过十字路口C(正在修路),共有多少种不同的走法?

解答：用标数法可以求出一共有120(种)走法.

以上是为大家分享的奥数计数问题之标数法经典例题讲解，希望希望同学们一定要每天坚持练习奥数题。同时希望大家能够在考试中取得优异的成绩！

相关推荐

备战2017小升初奥数数论问题知识点及例题分析总结 

小升初奥数常用的6种解题方法