备战2017小升初奥数染色问题知识点
编辑:sx_duxl
2016-12-22
做奥数题有助于我们能力的提升,不仅在数学方面,其他方面也是很有帮助的,主要是让我们多动脑思考。下面为大家分享小升初奥数染色问题知识点,希望对大家有帮助!
染色问题概念:
这里的染色问题不是要求如何染色,然后问有多少种染色方法的那类题目,它指的是一种解题方法。染色方法是一种将题目研究对象分类的形象化方法,通过将问题中的对象适当染色,我们可以更形象地观察分析出其中所蕴含的关系,再经过一定的逻辑推理,便能得出问题的答案。这类问题不需要太多的数学知识,但技巧性、逻辑性较强,要注意学会几种典型的染色方法。
染色问题基本解法:
三面涂色和顶点有关 8个顶点。
两面染色和棱长有关。即新棱长(棱长-2)×12
一面染色和表面积有关。同样用新棱长计算表面积公式(棱长-2)×(棱长-2)*6
0面染色和体积有关。用新棱长计算体积公式(棱长-2)×(棱长-2)×(棱长-2)
长方体的解法和立方体同理,即计算各种公式前长、宽、高都要先减2再利用公式计算。
经典例题:
例1、在平面上有一个27×27的方格棋盘,在棋盘的正中间摆好81枚棋子,他们被摆成一个9×9的正方形。按下面的规则进行游戏:每一枚棋子都可沿水平方向或竖直方向越过相邻的棋子,放进紧挨这枚棋子的空格中,并把越过的这个棋子取出来。问:是否存在一种走法,是棋盘最后恰好剩下一枚棋子?
分析解答:
分析游戏规则“每一枚棋子都可沿水平方向或竖直方向越过相邻的棋子,放进紧挨着这枚棋子的空格中,并把越过的这格棋子取出来”,可知:每走一步,走动棋子格、与它相邻被取出的棋子格、落子的空格,这三个格内棋子的状态,有或无,同时发生变化。因此可将整个棋盘按水平和竖直方向用三种颜色染色,开始时,
“棋盘的正中间摆好81枚棋子,它们被摆成一个9×9的正方形”,知三种颜色格子中棋子数是相同的(9×9/3=27),棋子数的奇偶性相同。由于每走一步,三种颜色格子里棋子数的奇偶性同时改变,因此三种颜色棋子数的奇偶性始终相同.
要使“棋盘上最后恰好剩下一枚棋子”,三种颜色的格子里棋子数2种颜色为0,1种颜色为1,两偶一奇,按上述走法显然是不可能的。
所以,不存在这样一种走法,使棋盘上最后恰好剩下一枚棋子。
练习题:
1、能否用一个“田”字和15个4×1长方形覆盖8×8棋盘?
2、能否用一个“田”字和15个“T”纸片,拼成一个8×8正方形棋盘?

3、下面三个图形都是从4×4的正方形分别剪去两个1×1的小方格得到的,问可否把它们分别剪成1×2的七个小长方形?

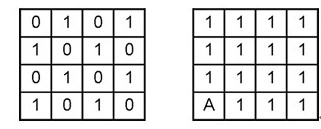
4、在左图中,对任意相邻的上下或左右2格中的数字同时加1或减1算作一次操作,经过若干次操作后变为右图。问:右图中A格中的数字是几?
适当的学习奥数可以锻炼思维,是大有好处的,以上是为大家分享的小升初奥数染色问题知识点,希望能够切实的帮助到大家!
相关推荐
标签:小升初奥数
免责声明
精品学习网(51edu.com)在建设过程中引用了互联网上的一些信息资源并对有明确来源的信息注明了出处,版权归原作者及原网站所有,如果您对本站信息资源版权的归属问题存有异议,请您致信qinquan#51edu.com(将#换成@),我们会立即做出答复并及时解决。如果您认为本站有侵犯您权益的行为,请通知我们,我们一定根据实际情况及时处理。