第九届华杯赛总决赛二试试题及解答
编辑:sx_wanghf
2014-04-10
第九届华杯赛总决赛二试试题及解答:
试题:
1.一正方形苗圃,栽种桃树和李树,一圈一圈地相间种植,即最外一圈种的是桃树,往内一圈是李树,然后是桃树,…,最内一圈种了4棵李树.已知树苗的的行距和列距都相等,桃树比李树多40棵.问:桃树和李树一共有多少棵?
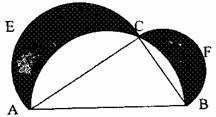
2.如右图,在以AB为直径的半圆上取一点C,分别以AC和BC为直径在△ABC外作半圆AEC和BFC.当C点在什么位置时,图中两个弯月型(阴影部分)AEC和BFC的面积和最大.
3、甲、乙两家医院同时接受同样数量的病人,每个病人患x病或y病中的一种,经过几天治疗,甲医院治好的病人多于乙医院治好的病人.问:经过这几天治疗后,是否可能甲医院对x病的治愈率和对y病的治愈率均低于乙医院的?举例说明.
(x病治愈率=![]() )
)
4、完成某项工程,甲单独工作需要18小时,乙需要24小时,丙需要30小时.现甲、乙和丙按如下顺序工作:甲、乙、丙、乙、丙、甲、丙、甲、乙、…,每人工作一小时换班,直到工程完成.问:当工程完成时,甲、乙、丙各干了多少小时?
5、求同时满足下列三个条件的自然数a,b:1)a>b; 2)![]() 3)a+b是平方数
3)a+b是平方数
6.如图,正方形跑道ABCD.甲、乙、丙三人同时从A点出发同向跑步,他们的速度分别为每秒5米、4米、3米.若干时间后,甲首次开始看到乙和丙都与自己在正方形的同一条边上,且他们在自己的前方.从此时刻算起,又经过21秒,甲乙丙三人处在跑道的同一位置,这是出发后三人第一次处在同一位置.请计算出正方形的周长的所有可能值.
解答:
1.400棵2.当C点在通过圆心且与直径AB垂直的直线与半圆的交点处时,两弯月型的面积最大3.能4.当工程完成时,甲干了7.2小时;乙、丙各干了8小时5. 6.正方形跑道的周长是210米或420米
1.解:下图画出苗圃的最里面3层,可以看出,苗圃所种果树的棵数为:4+12+20+28+……,每外一圈的桃树比相邻内一圈的李树多8棵,40÷8=5,所以共有10圈,最外圈的桃树为4+9×8=76棵,果树总棵数为 =400(棵)
2.解:两弯月形面积= + ×AC×BC= ×AC×BC
本题即AC×BC何时有最大值.因为 ,当 时, 有最大值,此时AC×BC有最大值,即AC=BC时,阴影面积最大.
3.解:例如,甲、乙医院接收和治愈x,y病的人数如下表:
甲医院
x病 y病 合计
接收人数 20 80 100
治愈人数 1 40 41
治愈率 5% 50%
乙医院
x病 y病 合计
接收人数 80 20 100
治愈人数 20 20 40
治愈率 25% 100%
4.解:三人各干一小时完成 ,360÷47=7 ,
即经过每人干7小时还剩工程的1- ×7= 没有干完,
从题目所给的换班规则(每次3小时,各干1小时),
每三次一个周期,三人的工作顺序第8次换班应和第二次相同,
即按乙、丙、甲的顺序, > , - = , > , - = ,
就是说,乙、丙又各干一小时,还剩 的工作量, ÷ =0.2(小时)
即当工程完成时,甲干了7.2小时;乙、丙各干了8小时.
5.解:由 ,可得:ab=169a+169b,ab-169a=169b,
a= ,a+b= = ,
因为a+b是平方数,所以b-169是平方数,设b-169= ,b= +169;
同理可得ab-169b=169a,b= ,a+b= = ,a-169是平方数,
设a-169= ,a= +169;于是,a+b= +2×169+ .
2×169=2×13×13,或2×169=2×1×169,或2×169=2×169×1,
因为a>b,所以m>n,a+b是平方数,
所以,m=169,n=1,a= +169= +169=169×170,b= +169= +169=170.
6.解:甲跑5圈孤时间,乙跑4圈,再跑3圈,此时三人处在同一位置,都在A点.倒退21秒,
甲的位置距A点5×21=105(米),甲与丙相距(5-3)×21=42(米).
因为此时甲首次看到乙、丙与自己在同一条边上,
所以甲此时应恰好在正方形的某一顶点上,即105米是正方形边长的整数倍,且正方形的边长不小于42米.
105÷1=105>42, 105÷2=52.5>42,105÷3=35<42.
所以正方形的边长是105米或52.5米,周长为420米或210米.
相关推荐:
标签:华杯赛
免责声明
精品学习网(51edu.com)在建设过程中引用了互联网上的一些信息资源并对有明确来源的信息注明了出处,版权归原作者及原网站所有,如果您对本站信息资源版权的归属问题存有异议,请您致信qinquan#51edu.com(将#换成@),我们会立即做出答复并及时解决。如果您认为本站有侵犯您权益的行为,请通知我们,我们一定根据实际情况及时处理。