第十一届华杯赛初赛试题及解答
编辑:sx_wanghf
2014-04-11
第十一届华杯赛初赛试题及解答:
1. 如图所示,将一张正方形纸片先由下向上对折压平,再由右翻起向左对折压平,得到小正方形ABCD,取AB的中点M和BC的中点N,剪掉△MBN,得五边形AMNCD。

则将折叠的五边形AMNCD纸片展开铺平后的图形是( )。
2. 2008006共有( )个质因数。
(A)4 (B)5 (C)6 (D)7
3、奶奶告诉小明:“2006年共有53个星期日”。聪敏的小明立到告诉奶奶:2007年的元旦一定是()。
(A)星期一 (B)星期二 (C)星期六 (D)星期日
4、如图,长方形ABCD中AB∶BC=5∶4。位于A点的第一只蚂蚁按A→B→C→D→A的方向,位于C点的第二只蚂蚁按C→B→A→D→C的方向同时出发,分别沿着长方形的边爬行。如果两只蚂蚁第一次在B点相遇,则两只蚂蚁第二次相遇在( )边上。
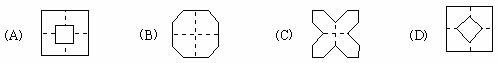
(A)AB (B)BC (C)CD
5、图中ABCD是个直角梯形(∠DAB=∠AB C=90°),以AD为一边向外作长方形ADEF,其面积为6.36平方厘米。连接BE交AD于P,再连接PC。则图中阴影部分的面积是()平方厘米。
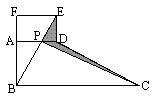
(A)6.36 (B)3.18 (C)2.12 (D)1.59
6、五位同学扮成奥运会吉祥物福娃贝贝、晶晶、欢欢、迎迎和妮妮,排成一排表演节目。如果贝贝和妮妮不相邻,共有( )种不同的排法。
(A)48 (B)72 (C)96 (D)120
二、A组填空题
7、在算式

中,汉字“第、十、一、届、华、杯、赛”代表1,2,3,4,5,6,7,8,9中的7个数字,不同的汉字代表不同的数字,恰使得加法算式成立。则“第、十、一、届、华、杯、赛”所代表的7个数字的和等于____。
8、全班50个学生,每人恰有三角板或直尺中的一种,28人有直尺,有三角板的人中,男生是14人,若已知全班共有女生31人,那么有直尺的女生有____人。
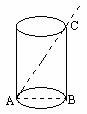
9、下图是一个直圆柱形状的玻璃杯,一个长为12厘米的直棒状细吸管(不考虑吸管粗细)放在玻璃杯内。当吸管一端接触圆柱下底面时,另一端沿吸管最少可露出上底面边缘2厘米,最多能露出4厘米。则这个玻璃杯的容积为____立方厘米。(取π=3 14)(提示:直角三角形中“勾6、股8、弦10”)
10、有5个黑色和白色棋子围成一圈,规定:将同色的和相邻的两个棋子之间放入一个白色棋子,在异色的和相邻的两个棋子之间放入一个黑色棋子,然后将原来的5个棋子拿掉。如果从图(1)的初始状态开始依照上述规定操作下去,对于圆圈上呈现5个棋子的情况,圆圈上黑子最多能有___个。

三、B组填空题
11、李大爷用一批化肥给承包的麦田施肥。若每亩施6千克,则缺少化肥300千克;若每亩施5千克,则余下化肥200千克。那么李大爷共承包了麦田___亩,这批化肥有___千克。
12、将从1开始的到103的连续奇数依次写成一个多位数:A=13579111315171921……9799101103。
则数a共有_____位,数a除以9的余数是___。
13、自制的一幅玩具牌共计52张(含4种牌:红桃、红方、黑桃、黑梅。每种牌都有1点、2点、……、13点牌各一张)。洗好后背面朝上放好。一次至少抽取____张牌,才能保证其中必定有2张牌的点数和颜色都相同。如果要求一次抽出的牌中必定有3张牌的点数是相邻的(不计颜色)。那么至少要取___张牌。
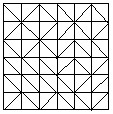
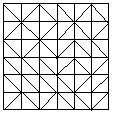
14、图中有____个正方形,有___个三角形。
1、D

解:考察空间想像力。如图,实际是逆向想像操作过程。
2、选C
解:因为20082006=2006×1000+2006=2006×1001=(2×17×59)×(7×11×13)。
3、选A
解:2006年有365天,而365=7×52+1,又已知2006年有53个星期天,只能元旦是星期天,且12月31日也是星期日,所以,2007年月的元旦是星期一。
4、选D

解:如图,长方形ABCD中AB∶BC=5∶4。将AB,CD边各5等分,BC,DA边各4等分。设每份长度为a。由于两只蚂蚁第一次在B点相遇,所以第一只蚂蚁走5a,第二只蚂蚁走4a,接下来,第一只蚂蚁由B走到E点时,第二只蚂蚁由B走到F点,再接下来,当第一只蚂蚁由走到G点时,第二只蚂蚁由F也走到G,这时,两只蚂蚁第二次相遇在DA边上。
5、选B
解:如图,连接AE,BD。因为AD∥BC,则:
![]()
又AB∥ED,则:
![]()
所以,
![]()
=3.18(平方厘米)
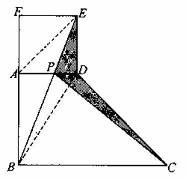
说明:答案和直角梯形形状无关,可以让BC边趋近AD边,直到和AD边重合,此时,P与A重合,PE是ADEF的对角线,所以,阴影部分的面积是ADEF面积的一半,等于3.18平方厘米。
6、B
解:贝贝在左、妮妮在右相邻的排法有4×3×2×1=24(种),贝贝在右、妮妮在左相邻的排法也有4×3×2×1=24(种),总的排法5×4×3×2×1=120(种)。所以贝贝和妮妮不相邻的排法是120-2×24=72(种)。
二、A组填空题
7、35
解:根据加法规则,“第”=1。“届+赛”=6或“届+赛”=16。若“届+赛”=6,只能是“届”、
“赛”分别等于2或4,此时“一十杯”=10只能“一”、“杯”分别为3或7。此时“十+华”=9,“十”、“华”分别只能取(1,8),(2,7),(3,6),(4,5),但1,2,3,4均已被取,不能再取。所以,“届+赛”=6填不出来,只能是“届+赛”=16,“十+华”+1=10,也就是“一 + 杯”=9 同时“十 + 华” =9。所以它们可以分别在(3,6),(4,5)两组中取值。
因此“第、十、一、届、华、杯、赛”所代表的7个数字的和等于1+9+9+16=35。
8、23
解:有三角板的学生共50-28=22(人),其中女生22-14=8(人),那么有直尺的女生有31-8=23(人)。
9、226.08.
解:如图,一个长为12厘米的直棒状细吸管放在玻璃杯内,另一端沿吸管最多能露出4厘米,表明直圆柱的高CB=12-4=8(厘米);另一端沿吸管最少可露出2厘米,表明直圆柱的轴截面矩形的对角线长为AC=12-2=10(厘米)。由直角三角形中“勾6、股8、弦10”的常识,可知圆柱底面圆的直径是6厘米,半径为3厘米。因此,这个玻璃杯的容积为(立方厘米)。

10、4
解:因为在异色棋子之间放黑子,圆周上只有5个棋子,必有相邻两个棋子是同色的,所以,不同能出现5个黑子。而第二次操作时圆周上就出现了4个黑子。所以,在各次操作过错成后,圆圈上呈现的5个围棋子中最多能有4个黑子。
三、B组填空题
11、500;2700
解:设麦田x亩,如每亩施6千克,则缺少300千克化肥,可知现有化肥为6x-300(千克);如每亩施5千克,则余下200千克化肥,可知现有化肥应为5x+200(千克)。由于现有化肥量是个定值,所以6x-300=5x+200,解得x=500(亩)。
现有化肥量是5×500+200=2700(千克)。
12、101;4
解:一位的奇数有5个,两位的奇数有45个,再加两个三位奇数,所以a是一个5+2×45+3×2=101(位)数。
从1开始的连续奇数被9除的余数依次为1,3,5,7,0,2,4,6,8,1,3,5,7,0,2,4,6,8,…,从1开始,每周期为9个数1,3,5,7,0,2,4,6,8的循环。因为(1+3+5+7+0+2+4+6+8)被9除余数为0,从1-89恰为5个周期,所以这个101位数a被9除的余数为1+3+5+7+0+2+4被9除的余数,等于4。
解法2:一个自然数被9除的余数和这个自然数所有数字之和被9除的余数相同,利用这条性质,a=13579111315171921……9799101103中13579的数字和被9除的余数是7,而111315171921……9799所有数字之和被9除的余数是0,101103的数字和被9除的余数是6。所以,a被9除的余数是(7+6)被9除的余数,是4。
13、27;37
解:对前一种情况,可取红、黑色的1、2、3、4、5、6、7、8、9、10、11、12、13点各1张,共13×2=26(张),那么再取一张牌,必定和其中某一张牌点数相同,于是就有2张牌点数和颜色都相同。这是最杯的情况,因此,至少要取27张牌,必能保证有2张牌点数、颜色都相同。
对后一种情况,有以下的搭配:
(1,2,3)、(4,5,6)、(7,8,9)、(10,11,12),13。
因而对涂阴影的9个数,四种花色的牌都取,这样可以取到(4×2+1)×4=36(张)牌,其中没有3张牌的点数是相邻的。
现在考虑取37张牌,极端情况下,这37张牌,有4张是13,则至少要有33张牌取自(1,2,3)、(4,5,6)、(7,8,9)、(10,11,12)四个抽屉,根据抽屉原则,必有9个数来自其中一个抽屉,这个抽屉中就一定有3张牌的点数相邻的。因此,至少要取37张牌。
14、95;155。
解:第1问,以面积大小数正方形,记最小的正方形面积为1;面积为1的正方形的个数:36;面积为2的正方形的个数:4;面积为4的正方形的个数:25;面积为9的正方形的个数:16;面积为16的正方形的个数:9;面积为25的正方形的个数4;面积为36的正方形的个数:1。所以,共有36+4+25+16+9+4+1=95(个)正方形。
第2问。方法1:以图中的最小的直角三角形为计数基本单位数三角形:
只有1个基本图形单位的三角形共72个;
由2个基本图形单位组成的三角形共37个;
由4个基本图形单位组成的三角形共30个;
由8个基本图形单位组成的三角形共4个;
由9个基本图形单位组成的三角形共10个;
由16个基本图形单位组成的三角形共2个;
所以图中共有三角形72+37+30+4+10+2=155(个)。
方法2:依三角形的斜边的长度数三角形。
(1)斜边和水平线成45度角的三角形,记这类三角形最小的斜边的长度为1:
长度为3的斜边共有:5条;长度为4的斜边共有:1条。
因为图中这类斜边每条带有2个三角形,所以共有 2×(36+15+5+1)=114(个)。
(2)斜边水平的三角形,从上向下:
斜边在第一条线有2个;斜边在第二条线有4个;斜边在第三条线有4个;斜边在第四条线有5个;斜边在第五条线有2个;斜边在第六条线有2个;斜边在第七条线有2个;
所以这种类型的三角形共有21个。
(3)斜边为垂直线的三角形,从左向右:斜边在第一条线有2个;斜边在第二条线有2个;斜边在第三条线有5个;斜边在第四条线有3个;斜边在第五条线有3个;斜边在第六条线有4个;斜边在第七条线有1个,所以这种类型的三角形共有20个。共有114+21+20=155(个)三角形。
相关推荐:
标签:华杯赛
免责声明
精品学习网(51edu.com)在建设过程中引用了互联网上的一些信息资源并对有明确来源的信息注明了出处,版权归原作者及原网站所有,如果您对本站信息资源版权的归属问题存有异议,请您致信qinquan#51edu.com(将#换成@),我们会立即做出答复并及时解决。如果您认为本站有侵犯您权益的行为,请通知我们,我们一定根据实际情况及时处理。