第十一届华杯赛决赛试题及解答
编辑:sx_wanghf
2014-04-11
第十一届华杯赛决赛试题及解答:
一、填空题
1、计算:
![]() ÷126.3=( )
÷126.3=( )
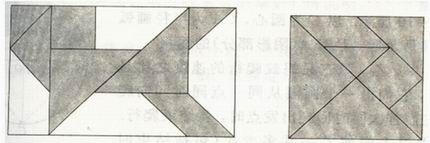
2、如图是一个长方形,其中阴影部分由一副面积为1的七巧板拼成(如图b)。那么这个长方形的面积是( )
3、有甲、乙、丙、丁四支球队参加的足球循环赛,每两队都要赛一场,胜得3分,负者得0分,如果踢平,两队各得1分。现在甲、乙、丙分别得了7分、1分和6分,已知甲和乙踢平,那么丁得( )分。
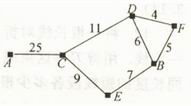
4、图中,小黑格表示网络的结点,结点之间的连线表示它们有网线要联,连续标注的数字表示该段网线单位时间内可以通过的最大的信息量。现在从结点A向结点B传递信息,那么单位时间内传梯的最大信息量是( )。
5、先写出一个两位数62,接着在62右端写这两个数字的和8,得到628,再写末两位数字2和8的和10,得到62810,用上述方法得到一个有2006位的整数:628101123…,则这个整数的数字之和是( )。
6、智慧老人到小明的年级访问,小明说他们年级共一百多名同学,老人请同学们按三人一行排队,结果多出一人,按五人一行排队,结果多出二人,按七人一行排队,结果多出一人,老人说我知道你们年级原人数应该是( )人。
7、如图所示,点B是线段AD的中点,由A,B,C,D四个点所构成的所有线段的长度均为整数,若这些线段的长度之积为10500,则线段AB的长度是( )。

8、100个非0自然数的和等于2006,那么它们的最大公约数最大可能值是( )。
二、解答下列各题
9、如图,圆O的直径AB与CD互相垂直,AB=10厘米,以C为圆心,CA为半径画弧。求月牙形ADBEA(阴影部分)的面积。
10、甲、乙、丙三只蚂蚁爬行的速度之比是8∶6∶5,它们沿一个圆圈从同一点同时同向爬行,当它们首次同时回到出发点时,就结束爬行。问蚂蚁甲追上蚂蚁乙一共多少次(包括结束时刻)?
11、如图,ABCD是矩形,BC=6cm, AB=10cm,AC和BD是对角线,图中的阴影部分以C为轴旋转一周,则阴影部分扫过的立体的体积是多少立方厘米?(π取3.14)
12、将一根长线对折,再对折,共对折10次,得到一束线,用剪刀将这束线剪成10等份,问:可以得到不同长度的短线段各多少根?
三、解答下列各题
13、华罗庚爷爷在一首诗文中勉励青少年:
“猛攻若战是第一,熟练生出百巧来,勤能补拙是良训,一分辛劳一分才。“
现在将诗文中不同的汉字对应不同的自然数,相同的汉字对应相同的自然数,并且不同汉字所对应的自然数可以排列成一串连续的自然数。如果这个28个自然数的平均值是23,问“分”字对应的自然数的最大可能值是多少?
14、一根长为L的木棍,用红色刻度线将它分成m等份,用黑色刻度将它分成n等份(m>n)。
(1)设x是红色与黑色刻度线重合的条数,请说明:x+1是m和n的公约数;
(2)如果按刻度线将该木棍锯成小段,一共可以得到170根长短不等的小棍,其中最长的小棍恰有100根。试确定m和n的值。
一、填空
1. 0.1 2. ![]() 3. 3 4. 17 5. 7018 6. 127 7. 5 8. 17
3. 3 4. 17 5. 7018 6. 127 7. 5 8. 17
二、解答下列各题,要求写出简要过程
9解:①月牙形ADBEA(阴影部分)的面积=半圆的面积+△ABC的面积-扇形 的面积
②月牙形ADBEA的面积= =25(平方厘米).
答:月牙形ADBEA的面积是25平方厘米。
10解:①甲乙丙三只蚂蚁的速度之比为8∶6∶5,所以,当它们首次同时回到出发点时,甲运动8圈,乙运动6圈。②蚂蚁甲比蚂蚁乙多运动了1圈,就追上蚂蚁乙1次,所以,甲一共追上乙2次。
答:当三只蚂蚁爬行结束时,甲追上乙2次。
1l解:①设三角形BCO以CD为轴旋转一周所得到的立体的体积是s,S等于高为10厘米,底面半径是6厘米的圆锥的体积减去2个高为5厘米,底面半径是3厘米的圆锥的体积。
②即: ,
2S=180π=565.2(立方厘米)
答:体积是565.2立方厘米。
12解:
①10次对折后,得到的是1024条线并列的线束。
②用剪刀将得到的线束剪成10等分,除去两端,中间的8等分的线段都是较短的线段,共有8×1024根。
③另外,剪下的两端,其中,有一端,有2条短的线段。余下(2×1024-2)条线,每两条构成1条线段。所以,较长的线段有1024-1=1023根,较短的线段共有8×1024+2=8194根。
答:较长的线段有1024-1=1023根,较短的线段共有8×1024+2=8194根。
三、解答下列各题,要求写出详细过程
13.解:①因为23×28=644,
②设这串连续自然数的起始的数是m,不同汉字所对应的自然数依次是:
m,m+1,…,m+23;设其中“分”字对应的自然数是m+x,“是”字对应m+a,“一”字对应m+b。既然要求“分”字对应的自然数尽可能大,可以要求23≥X>a>b≥0。
诗文中“分、是”各出现2次,“一”出现3次,其他汉字只出现1次,则有
=644,
28m+276+(a+2b)+x=644,28m=368-x-(a+2b)
③ , ,但是,
23≥x,b≥0,a+b≥1+0,a+2b=a+b+b≥1.
所以, <35.29.
取m=12,x=23,a=9,b=0(或a=5,b=2或a=1,b=4),得到满足条件的解,其中“分”对应的自然数是35。
答:“分”对应的自然数的最大可能值是35。
14.解:①
同样,
② 13+n是13×13的因数,13×13只有3个因数:1,13, .所以,
甲追上乙的位置(3分):③会判断丙在甲追上乙的时刻所爬行的距离(3分)。
即13+n是13×13的因数,13×13只有3个因数:1,13,13。所以,
13+n= ,n= -13=156,m=12。
求出正整m,n的另一方法:使 , .
设m=Ka,n=Kb,(a,b)=1,代入上式, .
(b一a)和a,b都互质,一定整除K。记d= 是正整数,b>a则有: .
由上式和b>a,b=13,a=1,d=1。所以,K=12,m和n有唯一解,m=13,n=156。
符:m=13,n=156。
相关推荐:
标签:华杯赛
免责声明
精品学习网(51edu.com)在建设过程中引用了互联网上的一些信息资源并对有明确来源的信息注明了出处,版权归原作者及原网站所有,如果您对本站信息资源版权的归属问题存有异议,请您致信qinquan#51edu.com(将#换成@),我们会立即做出答复并及时解决。如果您认为本站有侵犯您权益的行为,请通知我们,我们一定根据实际情况及时处理。