第十二届华杯赛总决赛一试试题及解答：

1.从下面每组数中各取一个数，将它们相乘，则所有这样的乘积的总和是___.

第一组：3/4 ，0.15;第二组：4，2/3 ;第三组：3/5 ，1.2

2.

一个正方体，平放于桌面，下图是从初始状态向不同方向翻滚一次所得到的三幅视图，则这个正方体初始状态的正面是___色，右面是___色.

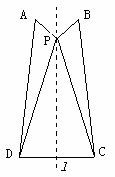
3.如图所示，已知APBCD是以直线l为对称轴的图形，且∠APD=116°，∠DPC=40°，DC>AB，那么，以A、P、B、C和D五个点为顶点的所有三角形中有___个钝角三角形，有___个锐角三角形.

4.A、B、C三项工程的工作量之比为1∶2∶3，由甲、乙、丙三个工程队分别承担，同时开工，若干天后，甲完成的工作量是乙未完成工作量的二分之一，乙完成的工作量是丙未完成工作量的三分之一，丙完成的工作量等于甲未完成的工作量，则甲、乙、丙三个队的工作效率的比是多少?

5.将1分、2分、5分和1角的硬币投入19个盒子中，使每个盒子里都有硬币，且任何两个盒子里的硬币的钱数都不相同。问：至少需要投入多少硬币?这时，所有的盒子里的硬币的总钱数至少是多少?

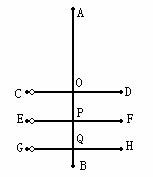
6.下图是一种电脑射击游戏的示意图，线段CD、EF和GH的长度都是20厘米，O、P、Q是它们的中点，并且位于同一条直线AB上，AO=45厘米，OP=PQ=20厘米，已知CD上的小圆环的速度是每秒5厘米，EF上的小圆环的速度是每秒9厘米，GH上的小圆环的速度是每秒27厘米。零时刻，CD、EF、GH上各有一个小圆环从左端点同时开始在线段上匀速往返运动。问：此时，从点A向B发射一颗匀速运动的子弹，要想穿过三个圆环，子弹的速度最大为每秒多少厘米?

1.解：设总和为S，则

S= 

=(0.75+0.15)×(

 )

 

=0.9×(2.4+4.8+0.4+0.8)

=0.9×8.4=7.56

2.解：红面与灰、蓝、棕、白面相邻，故知红面与绿面相对;同理可知白面与蓝面相对，灰面与棕面相对。

初始状态经翻滚后，上面不能仍为上面，故初始状态的上面不能为灰、绿、棕。初始状态的上面只可能是红，或蓝，或白。将题目所给的三幅视图中间的一幅：

翻滚一次可得以下四种状态：

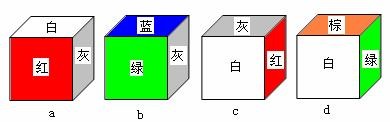
其中必有一种为初始状态，但灰、绿不能是初始状态的上面，故c、d不可能是初始状态。A向左翻滚得：

　　，

 

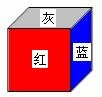
向右翻滚得：

　　，

 

而b的前面为绿面，绿面的对面是红面，经一次翻滚不能得到上述两种状态。

由此可知，初始状态为a，它的正面为红面，右侧为灰面。

3.解： =10，以A、P、B、C、D五个点可以形成10个三角形，这10个三角形的内角中，

 

∠APD=∠BPC=116°>90°，∠APC=∠BPD=116°+40=156>90°

∵DC>AB，故∠ADC与∠BCD为锐角，∠BAD与∠ABC为钝角，

∠APB=360°-116°×2-40°=88°<90°，

其余均为锐角。

故有6个钝角三角形，4个锐角三角形.

4.解：设三个队的工作效率分别为1/a 、1/b 、1/c ，三项工程的工作量分别为1、2、3，若干天为k天，

则k天后，甲完成的工作量为 k/a，未完成的工作量为1-k/a ，

乙完成的工作量为k/b ，未完成的工作量为2-k/b ，

丙完成的工作量为 k/b，未完成的工作量为3-k/b ，

于是有：

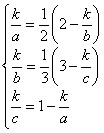
由此可得： 

从而可得：

 ，

即 ，

，进而得

 ，即 

，

 

∴ 

　5.解：只取一枚有1分、2分、5分、10分(1角)4种;

 

取二枚有1+1=2(分)，2+2=4(分)，5+5=10(分)，10+10=20(分)(2角)，

1+2=3(分)，1+5=6(分)，1+10=11(分)(1角1分)，

2+5=7(分)，2+10=12(分)(1角2分)，5+10=15(分)(1角5分)，

共10种，其中重复2种(2分、10分)，加上只取一枚的共12种不同币值;

取三枚时，可将以上取两枚的10种情况，分别加1分、2分、5分、10分，共有40种情况。从小到大取出7种不重复的币值为：8分、9分、13分、14分、16分、17分、21分，加上上述12种共19种。

公用硬币的枚数为：1×4+2×8+3×7=41(枚)

总钱数为：1+2+3+…+17+20+21=194(分)

6.解：小环过O点的时间为4k+2(k=0，1，2，…);

小环过P点的时间为 

(m=0，1，2，…);

 

小环过Q点的时间为 

(n=0，1，2，…);

 

由GH上小环的速度刚好为EF上小环的速度的3倍可知，当EF上的小环处于P点时，GH上的小环一定同时处于Q点，子弹经过P点小环后到达Q点，如果能穿过GH上小环，只能是GH上小环下1次，或下2次，或下3次，…再经过Q点，即子弹到达P点与到达Q点的时间差满足 ×n(n=1，2，3，…)，为 的整数倍。

由于OP=PQ，子弹匀速，所以，子弹从O到P，也应为 的整数倍。当k=0时， ，不论m取何值，均不为 的整数倍，只有当k=5x+2时(x=0，1，2，…) 的值满足 的整数倍。由于题目要取最大值，此时k应最小，取x=0，此时k=2。

当k=2时，小环到达O点时间为4k+2=10(秒)，子弹从A到O也应为10秒，速度为4.5厘米/秒。则子弹由A到P所用时间为 秒，即 = ，m=6;子弹由A到Q的时间为 秒，即 = ，n=25。

可知，当子弹速度为4.5厘米/秒时，可穿过三个环，且此为穿过三个环的最大速度。

相关推荐：

第十二届华杯赛初赛试题及解答  

第十一届华杯赛决赛试题及解答