这篇小学二年级数学知识点：找规律法是精品学习网特地为大家整理的，希望对大家有所帮助!

观察、搜集已知事实，从中发现具有规律性的线索，用以探索未知事件的奥秘，是人类智力活动的主要内容.

数学上有很多材料可用以来模拟这种活动、培养学生这方面的能力.

例1 观察数列的前面几项，找出规律，写出该数列的第100项来?

12345，23451，34512，45123，…

解：为了寻找规律，再多写出几项出来，并给以编号：

仔细观察，可发现该数列的第6项同第1项，第7项同第2项，第8项同第3项，…也就是说该数列各项的出现具有周期性，他们是循环出现的，一个循环节包含5项.

100÷5=20.

可见第100项与第5项、第10项一样(项数都能被5整除)，即第100项是51234.

例2 把写上1到100这100个号码的牌子，像下面那样依次分发给四个人，你知道第73号牌子会落到谁的手里?

解：仔细观察，你会发现：

分给小明的牌子号码是1，5，9，13，…，号码除以4余1;

分给小英的牌子号码是2，6，10，14，…，号码除以4余2;

分给小方的牌子号码是3，7，11，…，号码除以4余3;

分给小军的牌子号码是4，8，12，…，号码除以4余0(整除).

因此，试用4除73看看余几?

73÷4=18…余 1

可见73号牌会落到小明的手里.

这就是运用了如下的规律：

用这种规律预测第几号牌子发给谁，是很容易的，请同学们自己再试一试.

例3 四个小动物换位，开始小鼠、小猴、小兔和小猫分别坐在1、2、3、4号位子上(如下图所示).第一次它们上下两排换位，第二次左右换位，第三次又上下交换，第四次左右交换.这样一直交换下去，问十次换位后，小兔坐在第几号座位上?

解：为了能找出变化规律，再接着写出几次换位情况，见下图.

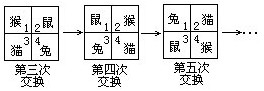
盯住小兔的位置进行观察：

第一次换位后，它到了第1号位;

第二次换位后，它到了第2号位;

第三次换位后，它到了第4号位;

第四次换位后，它到了第3号位;

第五次换位后，它又到了第1号位;

…

可以发现，每经过四次换位后，小兔又回到了原来的位置，利用这个规律以及10÷4=2…余2，可知：

第十次换位后，小兔的座位同第二次换位后的位置一样，即在第二号位.

如果再仔细地把换位图连续起来研究研究，可以发现，随着一次次地交换，

小兔的座位按顺时针旋转，

小鼠的座位按逆时针旋转，

小猴的座位按顺时针旋转，

小猫的座位按逆时针旋转，

按这个规律也可以预测任何小动物在交换几次后的座位.

例4 从1开始，每隔两个数写出一个数，得到一列数，求这列数的第100个数是多少?

1，4，7，10，13，…

解：不难看出，这是一个等差数列，它的后一项都比相邻的前一项大3，即公差=3，还可以发现：

第2项等于第1项加1个公差即

4=1+1×3.

第3项等于第1项加2个公差即

7=1+2×3.

第4项等于第1项加3个公差即

10=1+3×3.

第5项等于第1项加4个公差即

13=1+4×3.

…

可见第n项等于第1项加(n-1)个公差，即

按这个规律，可求出：

第100项=1+(100-1)×3=1+99×3=298.

例5 画图游戏先画第一代，一个△，再画第二代，在△下面画出两条线段，在一条线段的末端又画一个△，在另一条的末端画一个○;画第三代，在第二代的△下面又画出两条线段，一条末端画△，另一条末端画○;而在第二代的○的下面画一条线，线的末端再画一个△;…一直照此画下去(见下图)，问第十次的△和○共有多少个?

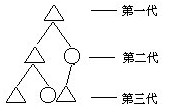
解：按着画图规则继续画出几代，以便于观察，以期从中找出图形的生成规律，见下图.

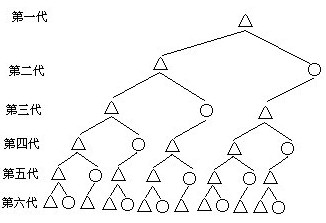
数一数，各代的图形(包括△和○)的个数列成下表：

可以发现各代图形个数组成一个数列，这个数列的生成规律是，从第三项起每一项都是前面两项之和.按此规律接着把数列写下去，可得出第十代的△和○共有89个(见下表)：

这就是著名的裴波那契数列.裴波那契是意大利的数学家，他生活在距今大约七百多年以前的时代.

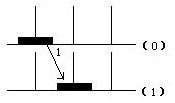
例6 如下图所示，5个大小不等的中心有孔的圆盘，按大的在下、小的在上的次序套在木桩上构成了一座圆盘塔.现在要把这座圆盘塔移到另一个木桩上.规定移动时要遵守一个条件，每搬一次只许拿一个圆盘而且任何时候大圆盘都不能压住小圆盘.假如还有第三个木桩可作临时存放圆盘之用.问把这5个圆盘全部移到另一个木桩上至少需要搬动多少次?(下图所示)

解：先从最简单情形试起.

①当仅有一个圆盘时，显然只需搬动一次(见下页图).

②当有两个圆盘时，只需搬动3次(见下图).

③当有三个圆盘时，需要搬动7次(见下页图).

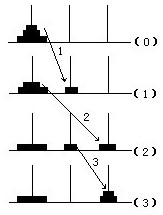
总结，找规律：

①当仅有一个圆盘时，只需搬1次.

②当有两个圆盘，上面的小圆盘先要搬到临时桩上，等大圆盘搬到中间桩后，小圆盘还得再搬回来到大圆盘上.所以小的要搬两次，下面的大盘要搬1次.这样搬到两个圆盘需3次.

③当有三个圆盘时，必须先要把上面的两个小的圆盘搬到临时桩上，见上图中的(1)～(3).由前面可知，这需要搬动3次.然后把最下层的最大圆盘搬一次到中间桩上，见图(4)，之后再把上面的两个搬到中间桩上，这又需搬3次，见图中(5)～(7).

所以共搬动2×3+1=7次.

④推论，当有4个圆盘时，就需要先把上面的3个圆盘搬到临时桩上，需要7次，然后把下面的大圆盘搬到中间桩上(1次)，之后再把临时桩上的3个圆盘搬到中间桩上，这又需要7次，所以共需搬动2×7+1=15次.

⑤可见当有5个圆盘时，要把它按规定搬到中间桩上去共需要：

以上就是由精品学习网为您提供的小学二年级数学知识点：找规律法，希望给您的写作带来帮助!

相关推荐：

新人教版二年级数学下册知识点复习