【摘要】在即将中考的时候，愿大家尽最大的可能复习好，因此，精品学习网中考频道为各位考生编辑了枣庄中考数学分类模拟试题：勾股定理，供大家阅读参考。

枣庄中考数学分类模拟试题：勾股定理

1、(2013•昆明)如图，在正方形ABCD中，点P是AB上一动点(不与A，B重合)，对角线AC，BD相交于点O，过点P分别作AC，BD的垂线，分别交AC，BD于点E，F，交AD，BC于点M，N.下列结论：

①△APE≌△AME;②PM+PN=AC;③PE2+PF2=PO2;④△POF∽△BNF;⑤当△PMN∽△AMP时，点P是AB的中点.

其中正确的结论有(　　)

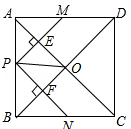
A.5个B.4个C.3个D.2个

考点：相似三角形的判定与性质;全等三角形的判定与性质;勾股定理;正方形的性质

分析：依据正方形的性质以及勾股定理、矩形的判定方法即可判断△APM和△BPN以及△APE、△BPF都是等腰直角三角形，四边形PEOF是矩形，从而作出判断.

解答：解：∵四边形ABCD是正方形，

∴∠BAC=∠DAC=45°.

∵在△APE和△AME中，

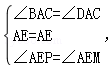
∴△APE≌△AME，故①正确;

∴

同理，

∵正方形ABCD中AC⊥BD，

又∵PE⊥AC，PF⊥BD，

∴∠PEO=∠EOF=∠PFO=90°，且△APE中AE=PE

∴四边形PEOF是矩形.

∴PF=OE，

∴PE+PF=OA，

又∵

，

∴PM+PN=AC，故②正确;

∵四边形PEOF是矩形，

∴PE=OF，

在直角△OPF中，OF2+PF2=PO2，

∴PE2+PF2=PO2，故③正确.

∵△BNF是等腰直角三角形，而△POF不一定是，故④错误;

∵△AMP是等腰直角三角形，当△PMN∽△AMP时，△PMN是等腰直角三角形.

∴PM=PN，

又∵△AMP和△BPN都是等腰直角三角形，

∴AP=BP，即P时AB的中点.故⑤正确.

故选B.

点评：本题是正方形的性质、矩形的判定、勾股定理得综合应用，认识△APM和△BPN以及△APE、△BPF都是等腰直角三角形，四边形PEOF是矩形是关键.

以上就是由精品学习网为您提供的枣庄中考数学分类模拟试题：勾股定理，愿您能取得优异的成绩。

相关推荐：

枣庄中考数学分类模拟试题：分解因式