中考数学答题技巧:圆与圆位置关系中常见辅助线的作法
编辑:sx_xiexh
2014-03-25
中考数学答题技巧:圆与圆位置关系中常见辅助线的作法
圆与圆位置关系是初中几何的一个重要内容,也是学习中的难点,本文介绍圆与圆的位置关系中常见的五种辅助线的作法。
1. 作相交两圆的公共弦
利用圆内接四边形的性质或公共圆周角,沟通两圆的角的关系。
例1. 如图1,⊙O1和⊙O2相交于A、B两点,过A、B分别作直线CD、EF,且CD//EF,与两圆相交于C、D、E、F。求证:CE=DF。
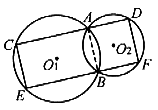
图1
分析:CE和DF分别是⊙O1和⊙O2的两条弦,难以直接证明它们相等,但通过连结AB,则可得圆内接四边形ABEC和ABFD,利用圆内接四边形的性质,则易证明。
证明:连结AB
因为
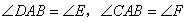
又
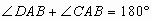
所以
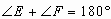
即CE//DF
又CD//EF
所以四边形CEFD为平行四边形
即CE=DF
2. 作两相交圆的连心线
利用过交点的半径、公共弦、圆心距构造直角三角形,解决有关的计算问题。
例2. ⊙O1和⊙O2相交于A、B两点,两圆的半径分别为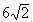 和
和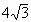 ,公共弦长为12。求
,公共弦长为12。求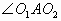 的度数。
的度数。
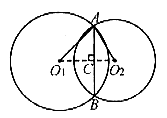
图2
分析:公共弦AB可位于圆心O1、O2同侧或异侧,要求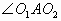 的度数,可利用角的和或差来求解。
的度数,可利用角的和或差来求解。
解:当AB位于O1、O2异侧时,如图2。
连结O1、O2,交AB于C,则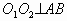 。分别在
。分别在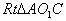 和
和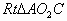 中,利用锐角三角函数可求得
中,利用锐角三角函数可求得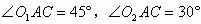
故
当AB位于O1、O2同侧时,如图3
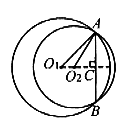
图3
则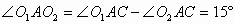
综上可知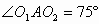 或
或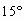
3. 两圆相切,作过切点的公切线
利用弦切角定理沟通两圆中角的关系
例3. 如图4,⊙O1和⊙O2外切于点P,A是⊙O1上的一点,直线AC切⊙O2于C,交⊙O1于B,直线AP交⊙O2于D。求证PC平分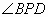 。
。
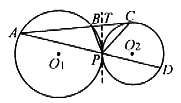
图4
分析:要证PC平分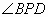 ,即证
,即证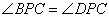 而
而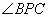 的边分布在两个圆中,难以直接证明。
的边分布在两个圆中,难以直接证明。
若过P作两圆的公切线PT,与AC交于T
易知
由弦切角定理,得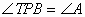
又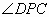 是
是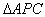 的一个外角
的一个外角
所以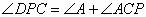
又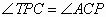
从而有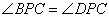
即PC平分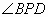
4. 两圆相切,作连心线
利用连心线经过切点的性质,解决有关计算问题。
例4. 如图5,⊙O1与半径为4的⊙O2内切于点A,⊙O1经过圆心O2,作⊙O2的直径BC,交⊙O1于点D,EF为过点A的公切线,若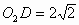 ,求
,求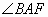 的度数。
的度数。
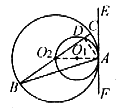
图5
分析:
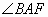 是弦切角,要求其度数,需将其转化为圆周角或圆心角,因此连结O1O2、O1A,则O1O2必过点A,且O2A为⊙O1的直径,易知
是弦切角,要求其度数,需将其转化为圆周角或圆心角,因此连结O1O2、O1A,则O1O2必过点A,且O2A为⊙O1的直径,易知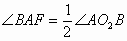 。
。
连结DA,则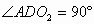 于是
于是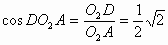
又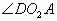 为锐角
为锐角
所以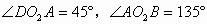
从而有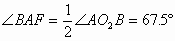
5. 过小圆圆心作大圆半径的垂线
有关公切线问题常过小圆的圆心作大圆半径的垂线,构造直角三角形。
例5. 如图6,⊙O1与⊙O2外切于点O,两外公切线PCD和PBA切⊙O1、⊙O2于点C、D、B、A,且其夹角为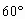 ,
,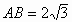 ,求两圆的半径。
,求两圆的半径。
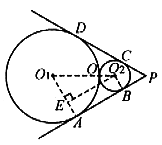
图6
分析:如图6,连结O1O2、O1A、O2B,过点O2作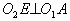 ,构造
,构造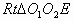 ,下面很容易求出结果。
,下面很容易求出结果。
请同学们自己给出解答。
(答案:两圆的半径分别为3和1)
相关推荐:
标签:中考数学答题技巧
免责声明
精品学习网(51edu.com)在建设过程中引用了互联网上的一些信息资源并对有明确来源的信息注明了出处,版权归原作者及原网站所有,如果您对本站信息资源版权的归属问题存有异议,请您致信qinquan#51edu.com(将#换成@),我们会立即做出答复并及时解决。如果您认为本站有侵犯您权益的行为,请通知我们,我们一定根据实际情况及时处理。