处，两直角边分别与

轴平行，纸板的另两个顶点

恰好是直线

与双曲线

的交点.

(1)求

和

的值;

(2)设双曲线

在

之间的部分为

，让一把三角尺的直角顶点

在

上

滑动，两直角边始终与坐标轴平行，且与线段

交于

两点，请探究是否存在点

使得

，写出你的探究过程和结论.

知识点：

解：(1)∵

在双曲线

上，

∥

轴，

∥

轴，

∴A，B的坐标分别

，

.

又点A，B在直线

上，∴

解得

或

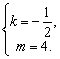
当

且

时，点A，B的坐标都是

，不合题意，应舍去;

当

且

时，点A，B的坐标分别为

,

,符合题意.

∴

且

.

(2)假设存在点

使得

.

∵

∥

轴，

∥

轴，∴

∥

，

∴

，∴Rt

∽Rt

,∴

,

设点P坐标为

(1

，

∴

.又

，

∴

，即

(※)

∵

.∴方程(※)无实数根.

所以不存在点

使得

相关推荐：

.2014年初三数学试题模拟试题精编  

初三数学下学期模拟试题