4.解：(1)∵a=2，b=1，c=-1，∴b²-4ac=1²-4×4×2(-1)=9>0，

∴方程有两个不相等的实数根.

(2)原方程变形为4x²-4x+1=0，

∵a=4，b=-4，c=1，

∴b²-4ac=(-4)²-4×4×1=16-16=0，

∴方程有两个相等的实数根.

(3∵a=7，b=2，c=3，b²-4ac=2²-4×7×3=-80<0，∴方程没有实数根.

*5.解：(1)∵a=1，b=-5，c=-6，b²-4ac=(-5)²-4×1×(-6)=49>0，

∴方程有两个不相等的实数根.

设方程的两个实数根分别为x_1，x_2.

由根与系数的关系，得x_1+x_2=-b/a=-5/3，x_1 x_2=c/a=1/3.

6解：(1)根据题意，得x²-13x+12=0，

所以x1=1，x_2=12，即当x=1或x=12时，代数式x²-13x+12的值等于0.

(2)由题意，得x²-13x+12=42，

所以x_1=15，x_2=-2，

所以当x=15或x=-2时，代数式x²-13x+12的值等于42.

(3)由题意，得x²-13x+12=-4x²+18，所以x_1=3，x_2=-2/5，

所以当x=3或x=-2/5时，代数式x²-13x+12的值与代数式-4x²+18的值相等.

7.解：设该公司这两年缴税的年均增长率为x，

由题意，得40(1+x)²=48.4.

解得x_1=0.1=10%，x_2=-2.1(舍去).

答:该公司这两年缴税的年均增长率为10%.

8.解：设原铁皮的边长为x cm，

则4(x-8)²=400.

解得x_1=18，x_2=-2(不合题意，舍去).

答：原铁皮的边长应为18cm.

9.解：如图2-7-3所示，设小路宽为 xm，由题意，得

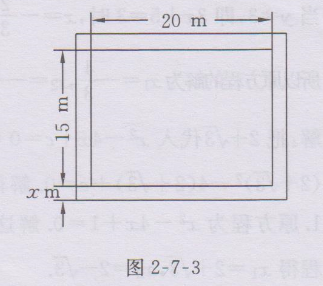
2x(15+2x)+2×20x=246.

整理，得2x²+35x-123=0.

解得x_1=3，x_2=-20.5(舍去).

答：小路的宽为3m.

10.解：设每行的座位数为x，则总行数为x+16，依题意，得x(x+16)=1 161.

(x-27)(x+43)=0.

解得x_1=27，x_2=-43(舍去).

答：每行的座位数为27.

11.解：设其中一段长为x cm，则另一段长为(56-x)cm.

(1)由(x/4)²+((56+x)/4)²=100，解得x_1=24，x_2=32，所以一段长为24cm，另一段长为32cm.

(2)由(x/4)²+((56-x)/4)²=196，解得x_1=0，x_2=56，所以不能剪开.

(3)由(x/4)²+((56-x)/4)^2=200，解得x_1=28+4√51>56(舍去)，

X_2=28-4√51<0(舍去).所以面积之和不可能等于200cm^2.

12.解：令3x+5=y，

原方程可化为y²-4y+3=0，

(y-1)(y-3)=0，解得y_1=1，y_2=3.

当y=1，即3x+5=1时，x=-4/3;

当y=3，即3x+5=3时，x=-2/3.

所以原方程的解为x_1=-4/3，x_2=-2/3.

13.解：把2+√3 代入x^2-4x+c=0中，得(2+√3)^2-4(2+√3)+c0.

解得c=1.原方程的另一个根为2-√3，c的值为1.

14.解：当s=200时，200=10t+3t²，解得t_1=20/3，t_2=-10(不合题意，舍去)，

所以行驶200m需要的时间为20/3 s.