误区提醒

(1)误认为梯形只有等腰梯形与直角梯形两种，而实质上这两种只是梯形的一个特殊情况;(2)对等腰梯形判定定理把握不准，忽视了“同一底”这一前提条件。

【典型例题】(2010年安徽省模拟)如图，在梯形ABCD中AD//BC,BD=CD,且∠ABC为锐角，若AD=4 ,BC=12，E为BC上的一点，当CE分别为何值时，四边形ABED是等腰梯形?直角梯形?写出你的结论，并加以证明。

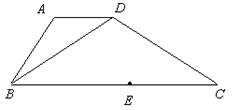
解：当CE=4时，四边形ABCD是等腰梯形

在BC上截取CE=AD,连接DE、AE.

又∵AD//BC, ∴四边形AECD是平行四边形

∴AE=CD=BD

∵BE=12-4=8>4, 即BE>AD

∴AB不平行于DE∴四边形ABED是梯形

∵AE//CD,CD=BD, ∴∠AEB=∠C=∠DBE[来源:学科网]

在△ABE和△DEB中

AE=DB, ∠AEB=∠DBE,BE=EB

△ABE≌△DEB(SAS) , ∴AB=DE

∴四边形ABED是等腰梯形

当CE=6,四边形ABED是直角梯形

在BC上取一点E,使得EC=BE=BC=6,连接DE,

∵BD=CD,∴DE⊥BC

又∵BE≠AD,AD//BE, ∴AB不平行于DE

∴四边形ABDE是直角梯形。

梯形知识点就到这儿了，体会每篇文章的不同，摘取自己想要的，友情提醒，理解最重要哦!!!