（二）探索新知

问题2：探究5

任意画出一个Rt△ABC，使∠C=90°，再画一个Rt△A′B′C′，使∠C′=90°，B′C′=BC，A′B′=AB，把画好的△A′B′C′剪下来，放到△ABC上，它们全等吗?

画法：

(1)画∠MC′N=90°;

(2)在射线C′M上截取B′C′=BC;

(3)以点B′为圆心，AB为半径画弧，交C′N于点A′;

(4)连接A′B′.

追问：作图的结果反映了什么规律?

你能用文字语言和符号语言概括吗?

文字语言： 斜边和一条直角边分别相等的两个直角三角形全等.(简写成“斜边、直角边”或“HL”)

符号语言：

在Rt△ABC与Rt△A′B′C′中，

∴Rt△ABC≌Rt△A′B′C′(HL).

师生活动：师生共同进行尺规作图，学生进行操作，观察是否全等.然后教师引导学生得出“斜边、直角边”判定方法，掌握文字和符号语言.

【设计意图】通过作图、剪图、比较图的过程让学生获得“斜边、直角边”的判定方法，培养学生发现问题的能力，锻炼学生用数学语言的能力.

（三）应用新知，解决问题

问题3：例5：如图，AC⊥BC，BD⊥AD，垂足分别为C，D，AC=BD. 求证：BC=AD

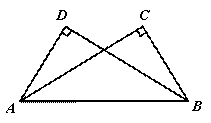
证明：∵AC⊥BC，BD⊥AD

∴∠C与∠D都是直角

在Rt△ABC与Rt△BAD′中，

∴Rt△ABC≌Rt△BAD(HL).

∴BC=AD.

追问：若图中AC，BD相交于点E，图中还有全等三角形吗?怎样证明?

师生活动：学生先口述理由，然后写出完整的证明过程，教师规范步骤.

【设计意图】让学生初步熟悉根据“HL”证明两个直角三角形全等的一般程序.同时意识到，除了“HL”，前面所学的判定也可以用来证明两个直角三角形全等.

（四）综合运用，巩固提高

问题4：完成教科书第43页练习1、2题.

1.如图，C是路段AB的中点，两人从C同时出发，以相同的速度分别沿两条直线行走，并同时到达D，E两地，DA⊥AB，EB⊥AB，D，E与路段AB的距离相等吗?为什么?

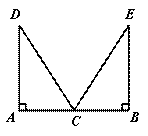
答： D，E与路段AB的距离相等.

证明： 由题意可知：DC=EC.

∵DA⊥AB，EB⊥AB，

∴∠A与∠B都是直角.

又∵C是路段AB的中点，

∴AC=BC.

在Rt△ACD与Rt△BCE中，

∴Rt△ACD≌Rt△BCE(HL).

∴AD=BE.