教师活动：

【导入】同学们对反证法这种间接证法不像学过的直接证法如综合法、分析法那样熟悉，感到抽象、难懂，让我们举出一例对反证法加以介绍.

我们年级有367名学生，请你证明这些学生中至少有两个学生在同一天过生日.

这个问题若用直接证法来解决是有困难的，我们可以运用反证法.

运用反证法证明这个问题首先是根据“至少有两个学生在同一天过生日”的反面是“任何两个学生都不在同一天过生日”，也就是反设“假设任何两个学生都不在同一天过生日”，从这个反设出发就会推出这

367人就会有不同的367天过生日，这就出现了与一年只有365天(闰年366天)的矛盾.产生这个矛盾的来源是由于开始的反设，因此反设不成立，这样得出了“至少有两个学生在同一天过生日”的结论.

设计意图：

以生活中的实际例子拉近学生与反证法的距离，激发学生的学习兴趣.

【板书】反证法证题的步骤：

1.反设;2.归谬;3.结论

【例】用反证法证明：圆的两条不是直径的相交弦不能互相平分.

已知：如图，在⊙O中，弦AB、CD相交于P点，且AB、CD不是直径.

求证：弦AB、CD不被P点平分.

【设问】用反证法证明这道题如何进行反设?怎样进行归谬?

【引导讨论】“弦AB、CD不被P点平分”的反面是“弦AB、CD被P点平分”，因而反设是“假设弦AB、CD被P点平分”.

学生活动：

思考后分组讨论，互相补充.

设计意图：

在关键处设问，激励学生探究精神，提高运用反证法的能力.

教师活动：

两条直线与OP都垂直，与垂线的性质矛盾.

结论是“弦AB、CD不被P点平分”成立.

这道题用反证法证明还有一个方法.

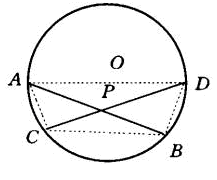
连结AD、BD、BC、AC·