教师：这位同学的想法和思路非常好，简直是一位天才

(同时再一次回顾该同学具体的做法)

教师：能否像求AC的方法一样对BC进行求解呢?

学生：可以

教师：那么具体应该怎么做呢?

学生：过点B向AC作高，垂直记作E，如图：

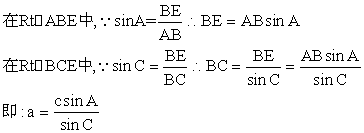
接下来，只需要将相关的数据代入即可求出BC的长度

教师：总结学生的做法

通过作两条高线后，即可把AC、BC的长度用已知的边和角表示出来

接下来，只需要将题目中的相关数据代入，本题便迎刃而解。

定理的发现：

教师：如果把本题目中的有关数据变一下，其中A=50o，B=80o大家又该怎么做

呢?

学生1：同样的做法(仍得作高)

学生2：只需将已知数据代入上述等式即可求出两边的长度

教师：还需要再次作高吗?

学生：不用

教师：对于任意的锐角三角形中的“已知两角及其夹边，求其他两边的长”的问

题是否都可以用上述两个等式进行解决呢?

学生：可以

教师：既然这两个等式适合于任意的锐角三角形，那么我们只需要记住这两个

等式，以后若是再遇见锐角三角形中的这种问题，直接应用这两个等式

并进行代入求值即可。

教师：大家看看，这两个等式的形式是否容易记忆呢?

学生：不容易

教师：能否美化这个形式呢?

学生：美化之后可以得到： (定理)

教师：锐角三角形中的这个结论，到底表达的是什么意思呢?

学生：在锐角三角形中，各边与它所对角的正弦的比相等

教师：那么锐角三角形中的这个等式能否推广到任意三角形中呢?那么接下来就

让我们分别来验证一下，看看这个等式在直角三角形和钝角三角形中是否

成立。

定理的探索：

教师：大家知道，在直角三角形ABC中：若

则：

所以：

故：

即： 在直角三角形中也成立

看完精品学习网高中频道推荐的高三数学正弦定理教案设计，相信老师对教学设计、规划也有了更清楚的掌握，更多参考资料尽在精品学习网。

精品学习网官方公众平台--【精品高中生】正式上线啦，大家可扫描下方的二维码关注，也可搜索微信号“gk51edu”或者直接输入“精品高中生”进行关注!!我们每天会为大家推送最新的内容哦~