【学生】合作讨论,得出什么为第一轮，第二轮。从而得到种病毒每一轮感染的计算机数构成的数列是1,20,202，203,…。③

【老师】回忆数列的等差关系和等差数列的定义，观察上面的数列①②③，说说它们有什么共同特点??引导学生类比等差关系和等差数列的概念，发现等比关系。我们可以发现：?

数列①从第2项起,每一项与它前一项的比都等于____;

数列②从第2项起,每一项与它前一项的比都等于____;

数列③从第2项起,每一项与它前一项的比都等于____;

也就是说这个数列有一个共同的特点：从第2项起,每一项与它前一项的比等于同一个常数。

我们把这样的数列称为等比数列。这就是我们今天要研究的课题，等比数列。

【设计意图】目的是让学生明白等比数列是来源于生活中的例子，观察所给各个数列的共同特点，进一步归纳出等比数列的定义。

二、探究新课

1、等比数列的定义

探究1：类比等差数列的定义，大家能否给等比数列下个定义？

【设计意图】学会类比的思想。

【学生】独立思考，类比等差数列的定义。给等比数列下定义。

如果一个数列从第2项起，每一项与它的前一项的比等于同一个常数，那么这个数列就叫做等比数列。这个常数叫做等比数列的公比。公比通常用字母q表示。

【老师】用数学符号语言怎样表示等比数列的定义呢?如果我们第n项用

表示，那么它的前一项该怎么表示，那么比怎么表示?这里的n的取值范围呢?

【学生】讨论，交流。

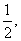
或

【老师】请同学们打开课本，看看课本上是怎样给等比数列下定义的，和刚才那位同学下的定义一样吗?有什么不同?

【学生】阅读课本，仔细对比，找出不同。学生发现课本中有q≠0这个条件.

思考：等比数列的定义中，可否去掉“q≠0”的条件?为什么?能否将“ ”的条件改写成“ ”?为什么?

【设计意图】引导学生对等比数列内涵再认识和进一步理解。

【学生】讨论，辨析，得到结论，不能去掉“q≠0”的条件，因为如果q=0,则分子为0,而每一个分子都可能出现在分母中,则分母为0无意义; 表达式说明在等比数列中的任意项都不能为0.

感悟:等比数列中q≠0,

.

【老师】那么是否存在既是等差又是等比的数列呢?

【学生1】常数列。

【老师】是吗?有不同意见吗?

【学生2】非零的常数列既是等差又是等比数列。

练习1：判断下列数列是否为等比数列，若是，请指出公比q。

(1) 1,2, 8，32，128,… 。 ---不 是

(2) -1,-5，-25，-125,…。 -- 是 q =5

(3)　2，2，2，2，… 。 --- 是　q =1

(4) 1，-0.5，0.25，-0.125，… 。 --- 是　q = - 0.5

(5) 1, 2，1, 2,1, 2…。 --- 不是

【老师】思考:公比q的取值范围是什么呢?

【学生】正数、负数，但是不能为零。

练习2：求下列各组数中插入怎样的数后是等比数列。

(1)1， ____ ， 9

(2)-1，____ ，-4

(3)-12，____ ，-3

(4)1， _____ ，1

【学生1】根据等比数列的定义，得出插入3后，构成等比数列。

【学生2】补充插入-3后，也能构成等比数列。学生思考，得到两个都符合题意.。

下面三个小题可根据(1)，顺利得到答案。

【老师】在学习等差数列的定义后，我们也做过这样的题目，在两数中间插入一个数，使三数成等差数列，那么我们把中间这个数称为等差中项。类比等差中项的概念，我们把刚才插入的那个数称为等比中项。

2、等比中项

探究2：前面的等差数列一节里我们有等差中项的定义，你能仿照等差中项，给出等比中项的定义吗？等差中项与等比中项有何差异？

【老师】类比等差中项的概念，大家给等比中项下个定义吧。

【学生】如果在a与b中间插入一个数G，使a，G，b成等比数列，那么G叫做a与b的等比中项。学生思考得结论：任何两个数都有等差中项，有且只有一个，而只有同号的两个数才有等比中项，而且有两个，且互为相反数。

3、等比数列的通项公式

我们继续来研究一下情境中的这三个数列。

探究3：试着写出上面三个数列的通项公式，并猜想等比数列的通项公式。

【设计意图】体现由特殊到一般的思想，先写出具体实例的通项公式，使学生经历观察，归纳，猜想的过程。

①

②

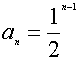
③

【学生】通过观察，看出这三个数列的通项公式，并寻找这三个公式中共性的地方，把①改写成

，②

，③

，观察，发现都有n-1次幂的形式，而且乘号前面的数字2,1,1都是首项

，乘号后面的数字2，

20都是各项的公比，所以猜想等比数列的通项公式是an=a1qn-1。

【老师】这位同学猜想的很好，那我们就来推导一下等比数列的通项公式，看看和这位同学猜想的一致吗?