【二年级】

课内知识：植树节到了，老师带着同学们去种树，要求大家把6棵树种成3条直线，每条直线上都有3棵树，你知道怎么种才能是老师的要求吗?

解答：如图

。

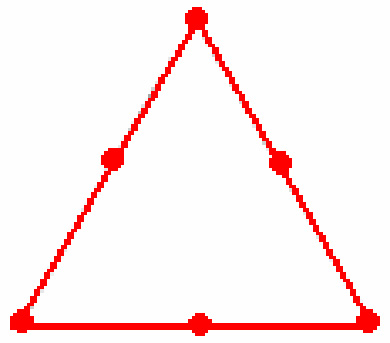
课外趣题：有20个小朋友排成一排，第一次从左到右1至3循环报数，第二次从左到右1至4循环报数，请问既报过1又报过4的小朋友都多少人?

解答：

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

【三年级】

课内知识：如果把1到999这些自然数按照从小到大的顺序排成一排，这样就组成了一个多位数：12345678910111213…996997998999。那么在这个多位数里，从左到右的第2000个数字是多少?

解答：一位数1—9共有9个;二位数10—99共有90个，占90×2=180位;一、二位数共占了189 位;2000-9-180=1811，这1811个数字都是三位数的，1811÷3=603……2，说明第2000个数是第604个三位数的第2位，三位数从100开始，第604个应该是603，第二位就是0。因此，从左到右的第2000个数字是0。

课外趣题：标有A，B，C，D，E，F，G记号的7盏灯顺次排成一行，每盏灯各安装着一个开关。现在A，C，D，G这4盏灯亮着，其余3盏灯是灭的。小方先拉一下A开关，然后拉B，C，…，直到G的开关各一次，接下去再按从A到G顺序拉动开关，并依此循环下去。他这样拉动了1990次后，亮着的灯是哪几盏?

解答：如果一个灯的开关被拉了2下，那么，这个灯原来是什么状态，还应该是什么状态，即原来亮着的还亮着，原来不亮的还是不亮。现在共有7盏灯，每个拉2次的话就是14次。也就是说，每拉14下，每个灯都和原来的情况一样。1990÷14=142……2，说明，拉1990次就相当于只拉了2次，那么就应该是A和B各被拉了一下。A原来亮着，现在变灭;B原来不亮，现在变亮。所以，拉1990次后亮着的灯应该有：B、C、D、G。

【四年级】

课内知识：甲、乙、丙三只盘子里分别盛着6个苹果。小明按下面的方法搬动5次：

第1次，把1个苹果从一只盘子里搬到另一只盘子里去;

第2次，把2个苹果从一只盘子里搬到另一只盘子里去;

第3次，甲盘不动，把3个苹果从一只盘子里搬到另一只盘子里去;

第4次，乙盘不动，把4个苹果从一只盘子里搬到另一只盘子里去;

第5次，丙盘不动，把5个苹果从一只盘子里搬到另一只盘子里去。

最后发现，甲、乙、丙三只盘子里依次盛有4，6，8个苹果。你知道小明是怎样搬动的吗?

解答：利用倒推的思想，第2次结束后，每盘里的苹果数可能为(5，4，9)或(13，4，1)。通过试验可以发现，显然第2次结束后只有(5，4，9)成立，因此搬动过程是唯一的。(6，6，6)→(5，6，7)→(5，4，9)→(5，1，12)→(9，1，8)→(4，6，8)

课外趣题：小明共有贰分和伍分硬币208枚。小明从中取出两枚硬币放在手中作为标准，剩余硬币两枚一组分成103组，每组得到一个币值和。他发现有67组的币值和比他手中币值和大，有12组的币值和比他手中币值和小，有24组的币值和与他手中币值和相等，那么208枚硬币的币值总和是多少分?

解答：67×(5+5)+(24+1)×(2+5)+12×(2+2)=893(分)

【五年级】

课内知识：从1、2、3、4、…、19、20这20个自然数中，至少任选几个数，就可以保证其中一定包括两个数，它们的差是12?

解答：20个自然数中，差是12的有以下8对：

{20，8｝，{19，7｝，{18，6｝，{17，5｝，{16，4｝，{15，3｝，{14，2｝，{13，1｝。

另外还有4个不能配对的数{9｝，{10｝，{11｝，{12｝，共制成12个抽屉(每个括号看成一个抽屉).只要有两个数取自同一个抽屉，那么它们的差就等于12，根据抽屉原理至少任选13个数，即可办到(取12个数：从12个抽屉中各取一个数(例如取1，2，3，…，12)，那么这12个数中任意两个数的差必不等于12)。

课外趣题：123456789101112……484950是一个多位数，从中划去80个数字，使剩下的数字(先后顺序不变)组成最大的多位数，这个最大的多位数是多少?

解答：123456789101112……484950，共有数字：9+2×(50-10+1)=91 (个)，从中划去80个数字，剩下的数字有：91-80=11(个)，组成一个11位数，题目要求这个11位数是最大的，当然要尽量保留数字9。

这个多位数有5个9，若要让5个9连在一起，就不能组成一个11位数，所以最右边的9不能保留。

保留4个9，后面也不能取8，否则这个数就不是11位数。保留4个9，后面如果是7，刚好组成一个11位数，因此，所求的最大11位数是99997484950。