20.如图，已知⊙O的弦AB、CD相交于点P，PA=4，PB=3，PC=6，EA切⊙O于点A，AE与CD的延长线交于点E，AE=2

5 ，那么PE的长 .

三、解答题(共11小题，满分75分)

21.计算： 1

3 +

2 −(

3 )0+2cos45°−3tan30°.

22.解不等式组：

3x−5 2 ≤x−2 3(x−1)<4(x+2)−5 并把解集在数轴上表示出来.

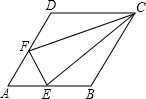
23.已知：如图，菱形ABCD中，E、F分别是AB、AD上的点，且AE=AF.

求证：CE=CF.

☆☆☆☆☆

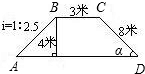
24.如图，拦水坝的横断面为梯形ABCD，根据图示数据求：

(1)坡角α;

(2)坝底宽AD和斜坡AB的长.(计算过程和结果都不取近似值)

☆☆☆☆☆

25.列方程(组)解应用题：

从A站到B站有120千米.一辆客车和一辆货车同时从A站出发，1小时后，客车在货车前面24千米;客车到达B站比货车早25分钟.求客车和货车每小时各走多少千米?

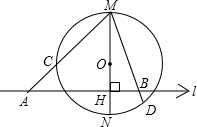
26.已知：如图，MN为⊙O的直径，l⊥MN于H，割线MCA及弦MBD分别交⊙O于C、D.

求证：MA•MC=MB•MD.

27.化简：( x3+8 x2+4x+4 − x3−8 x2−4 )÷ x3−6x2+9x x2−x−6

28.m为何整数时，关于x的方程3x2+6x+m=0有两个负实根?

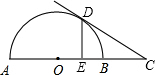
29.如图，AB是半圆的直径，O是圆心，C是AB延长线上一点，CD切半圆于D，DE⊥AB于E.已知AE：EB=4：1，CD=2，求BC的长.

30.已知：如图，AB和AC与⊙O相切于B、C，P是⊙O上一点，且PE⊥AB于E，PD⊥BC于D，PF⊥AC

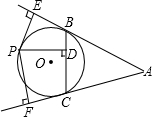
于F.

求证：PD2=PE•PF.

31.已知直线y= 1 2 x和y=-x+m，二次函数y=x2+px+q的图象的顶点为M.

(1)若M恰好在直线y= 1 2 x与y=-x+m的交点处，试证明：无论m取何实数值，二次函数y=x2+px+q的图象与直线y=-x+m总有两个不同的交点.

(2)在(1)的条件下，若直线y=-x+m过点D(0，-3)，求二次函数y=x2+px+q的表达式，并作出其大致图象.

(3)在(2)的条件下，若二次函数y=x2+px+q的图象与y轴交于点C，与x轴的左交点为A，试在

直线y= 1 2 x上求异于M的点P，使点P在△CMA的外接圆上.

这篇1999年四川省成都市中考数学试卷就和大家分享到这里了，愿您能够顺利走进自己梦想的学府!

相关推荐：

2007年四川省成都市中考数学试卷

2008年四川省成都市中考数学试卷