8.关于x的一元二次方程(a-1)x2+x+|a|-1=0的一个根是0，则实数a的值为(　　)

A.-1 B.0 C.1 D.-1或1

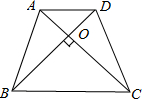
9.如图.梯形ABCD中，AD∥BC、AB=CD，AC丄BD于点O，∠BAC=60°，若BC=

6 ，则此梯形的面积为(　　)

A.2 B.1+

3 C.

2 +

6 D.2+

3

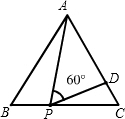
10.如图，等边三角形ABC的边长为3，点P为BC边上一点，且BP=1，点D为AC边上一点，若∠APD=60°，则CD的长为(　　)

A. 1 2 B. 2 3 C. 3 4 D.1

二、填空题(本大题共5小题，每小题4分，共20分)

11.若

x−1 在实数范围内有意义，则x的取值范围是 .

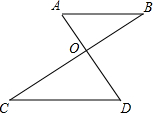
12.如图，AD与BC相交于点O，AB∥CD，若∠B=30°，∠D=60°.则∠BOD= 度.

13.正比例函数y=kx的图象反比例函数y= m x 的图象有一个交点的坐标是(-1，-2)，则另一个交点的坐标是 .

14.某居民小区为了了解本小区100户居民家庭平均月使用塑料袋的数量情况，随机调査了10户居民家庭月使用塑料袋的数量，结果如下(単位：只)

65  70  85  74  86  78  74  92  82  94

根据统计情况，估计该小区这100户家庭平均使用塑料袋为 只.

15.按如下程序进行运算：

并规定：程序运行到“结果是否大于65”为一次运算，且运算进行4次才停止，则可输入的整数x的个数是 .

三、解答题(本大题I～V，共9小题，共90分)

16.先化简，再求值：2(x+1)-(x+1)2，其中x=

3 .

17.解方程： 1 x−1 = 3 2x−2 +1.

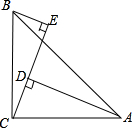
18.如图，在△ABC中，∠ACB=90°，AC=BC，BE⊥CE于点E.AD⊥CE于点D.

求证：△BEC≌△CDA.

19.某商场销售一种进价为20元/台的台灯，经调查发现，该台灯每天的销售量w(台)，销售单价x(元)满足w=-2x+80，设销售这种台灯每天的利润为y(元).

(1)求y与x之间的函数关系式;

(2)当销售单价定为多少元时.毎天的利润最大?最大利润多少?

(3)在保证销售量尽可能大的前提下.该商场每天还想获得150元的利润，应将销售单价定位为多少元?