本环节教师要注重培养学生的说理意识和能力.注重在探究说理中实现师生互动、生生互动的学习方式.体现了从合情推理到初步的演绎推理的思维推进.

归纳体会

引导学生体会平行四边形性质分别是从哪些角度阐述的?在探究过程中都用到了哪些方法?研究其他四边形性质时可类比平行四边形性质.

教师引导学生体会：解决线段相等、角相等问题的新方法——平行四边形的性质.

本环节通过对平行四边形从角、边、对角线、对称性等方面性质的归纳，有助于学生从不同角度来探究问题的意识形成，引导学生采用类比平行四边形性质的方法去研究其他特殊四边形的性质.

性质应用

例题：在□ABCD中, ∠B=140° ,求其他内角的度数.(学生板演、讲解)

变式：在□ABCD中，已知 ∠B+∠D=280°，求其他两个内角的度数.

教学过程

此题是巩固平行四边形对角相等的性质.

变式的目的是渗透转化思想.

设计说明

性质应用

总结提升：如果平行四边形一个内角的度数是已知的，就能确定其他三个内角的度数.

练习1.已知□ABCD的周长是20㎝，△ABC的周长是18㎝，则AC的长度是多少?

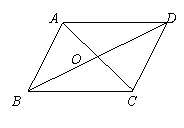
练习2.已知点O是□ABCD两条对角线的交点，对角线AC=6cm，BD=10 cm，则BC的取值范围是 .

若BC=7cm，则△OAD的周长是 .

注意引导学生从特殊到一般地思考问题.

此题是巩固平行四边形对边相等的性质.

此题是平行四边形性质的综合运用，锻炼了学生的说理能力.

收获与

感悟

学生先独立思考这节课的收获，再在小组内交流，最后全班交流.

本环节使学生的知识、方法在反思中得到巩固、升华.

作

业

1. 课本

练习1;习题1、2

2.(思考题)一块平行四边形土地，在对角线AC上有一口井E，连结BE、DE，现将两块地△BCE、

△DCE分给两农户，这样分公平吗?为什么?

由于本节重点探究了平行四边形的性质，所以创设了有一定思考深度的应用性思考作业，这是平行四边形性质的应用

通过对初三数学平行四边形及其性质教案设计的学习，希望对老师有所帮助，提供更多的教学参考内容。

相关推荐：

冀教版初三上册数学方程的近似解教案范文  

冀教版初三上册数学用一元二次方程解决实际问题教案范文