显示解析

17.在△AnBnCn中，记角An、Bn、Cn所对的边分别为an、bn、cn，且这三角形的三边长是公差为1的等差数列，若最小边an=n+1，则 lim n→∞ Cn=(　　)

A. π 2 B. π 3 C. π 4 D. π 6

显示解析

18.如图1，一个密闭圆柱体容器的底部镶嵌了同底的圆锥实心装饰块，容器内盛有a升水.平放在地面，则水面正好过圆锥的顶点P，若将容器倒置如图2，水面也恰过点P.以下命题正确的是(　　)

A.圆锥的高等于圆柱高的 1 2

B.圆锥的高等于圆柱高的 2 3

C.将容器一条母线贴地，水面也恰过点P

D.将容器任意摆放，当水面静止时都过点P

显示解析

三、解答题(满分74分)

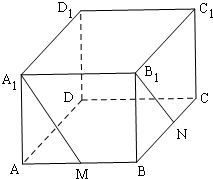
19.如图在长方体ABCD-A1B1C1D1中，AB=a，AD=b，AC1=c，点M为AB的中点，点N为BC的中点.

(1)求长方体ABCD-A1B1C1D1的体积;

(2)若a=4，b=2，c=

21 ，求异面直线A1M与B1N所成的角.

显示解析

20.已知A

cosα，sinα

.B

cosβ，sinβ

，其中α、β为锐角，且|AB|=

10 5 .

(1)求cos(α-β)的值;

(2)若tan α 2 = 1 2 ，求cosα及cosβ的值.

显示解析

21.数列{an}是递增的等差数列，且a1+a6=-6，a3•a4=8.

(1)求数列{an}的通项公式;

(2)求数列{an}的前n项和Sn的最小值;

(3)求数列{|an|}的前n项和Tn.

显示解析

22.已知圆C过定点A(0，1)，圆心C在抛物线x2=2y上，M、N为圆C与x轴的交点.

(1)当圆心C是抛物线的顶点时，求抛物线准线被该圆截得的弦长.

(2)当圆心C在抛物线上运动时，|MN|是否为一定值?请证明你的结论.

(3)当圆心C在抛物线上运动时，记|AM|=m，|AN|=n，求 m n + n m 的最大值，并求出此时圆C的方程.

显示解析

23.设函数fn(x)=−2n+ 2 x + 22 x2 +…+ 2n xn .

(1)求函数f2(x)在

1，2

上的值域;

(2)证明对于每一个n∈N*，在

1，2

上存在唯一的xn，使得fn(xn)=0;

(3)求f1(a)+f2(a)+…+fn(a)的值.

上海市虹口区高考数学一模试卷就介绍到这里了，更多精彩内容请继续关注精品学习网!

相关推荐：

2014年青岛市高三数学一模理科试题(含答案) 

2014淄博高三数学一模文科试卷(含答案)