2015年三明市高一上册数学期末试卷及答案
编辑:
2015-06-26
20、(本小题满分9分)
解:(I)![]()
因为![]()
所以,![]()
![]()
故 ![]() …………4分
…………4分
(II)因为向量![]() 与向量
与向量![]() 共线,
共线,![]() ,
,![]() 所以,
所以,![]() ,
,![]() ,…………6分
,…………6分
![]()
![]() ………7分
………7分
故,当![]() 时,
时,![]() 取最大值4,此时,
取最大值4,此时,![]()
所以,![]() …………9分
…………9分
考查平面向量的共线、垂直、数量积概念和平面向量的坐标运算,考查二次函数的最值与平面向量、三角函数知识的综合运用能力、化归与转化和函数与方程思想。
21、(本小题满分10分)
解:(I)当![]() 时,
时, ![]() ,因为
,因为![]() ,故
,故![]() 为奇函数;
为奇函数;
当![]() 时,
时,![]() 为非奇非偶函数………2分
为非奇非偶函数………2分
(II)当![]() 时,
时,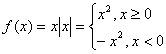 故函数
故函数![]() 的增区间
的增区间![]() ……3分
……3分
当![]() 时,
时,![]() 故函数
故函数![]() 的增区间
的增区间![]() ,函数
,函数![]() 的减区间
的减区间![]()
………5分
(III)①当![]() 即
即![]() 时
时![]() ,
,![]() ,
,![]() 当
当![]() 时,
时,![]() ,
,![]() 的最大值是
的最大值是![]() 当
当![]() 时,
时,![]() ,
,![]() 的最大值是
的最大值是![]() ………7分
………7分
②当![]() 即
即![]() 时,
时,![]() ,
,![]() ,
,![]() ,
,![]() 所以,当
所以,当![]() 时,
时,![]() 的最大值
的最大值![]() ………9分
………9分
综上,当![]() 时,
时, ![]() 的最大值是
的最大值是![]() 当
当![]() 时,
时,![]() 的最大值是
的最大值是![]() ………10分
………10分
考查分段函数的奇偶性、单调性和最值问题的综合运用能力,考查数形结合、分类与整合思想。
上述提供的上册数学期末试卷希望能够符合大家的实际需要!
相关推荐:
标签:高一数学试题
免责声明
精品学习网(51edu.com)在建设过程中引用了互联网上的一些信息资源并对有明确来源的信息注明了出处,版权归原作者及原网站所有,如果您对本站信息资源版权的归属问题存有异议,请您致信qinquan#51edu.com(将#换成@),我们会立即做出答复并及时解决。如果您认为本站有侵犯您权益的行为,请通知我们,我们一定根据实际情况及时处理。