教案是老师为讲授新一课而做的教学设计和设想，编写教案要依据教科书和教学大纲，从学生的实际出发，精心设计，精品学习网准备了高三数学简单线性规划问题教案设计，希望对大家有用。

一、教学内容解析

线性规划是运筹学中研究较早、发展较快、应用广泛、方法较成熟的一个重要分支，是辅助人们进行科学管理的数学方法，为合理地利用有限的人力、物力、财力等资源作出最优决策.

本节的教学重点是线性规划问题的图解法.数形结合和化归思想是研究线性约束条件下求线性目标函数的最值问题的数学理论和方法,本节教学内容中蕴含了丰富的属性结合素材，具体表现为:(1)不定方程的解与平面内点的坐标的结合，进而产生了直线的方程.(2)线性目标函数解析式与直线的斜截式方程的结合.(3)线性目标函数的函数值与直线的纵截距的结合.(4)二元一次不等式(组)与为平面内点的坐标的结合.(5)线性目标函数在线性约束条件下的最值与直线过可行域内的点时纵截距的最值的结合.这样就能使学生对数形结合思想的理解和应用更透彻,为以后解析几何的学习和研究奠定了基础, 使学生从更深层次地理解“以形助数”的作用。

二、教学目标设置

(1)知识与技能：使学生了解二元一次不等式表示平面区域;了解线性规划的意义以及约束条件、目标函数、可行解、可行域、最优解等基本概念;理解线性规划问题的图解法，并能应用它解决一些简单的实际问题;

(2)过程与方法：在实验探究的过程中，培养学生的数据分析能力、探究能力、合情推理能力;在应用图解法解题的过程中，培养学生运用数形结合思想解题的能力。

(3)情态、态度与价值观：让学生体会数学源于生活，服务于生活;体会数学活动充满着探索与创造，培养学生动手操作、勇于探索的精神。

教学重点 :求线性规划问题的最优解

教学难点 :学生对为什么要将求目标函数的最值问题转化为经过可行域的直线在y轴上的截距的最值问题以及如何想到这样转化存在疑惑，在教学中应紧扣实际，突出知识的形成发展过程。

三、学生学情分析

本节课学生在学习了不等式、直线方程的基础上，通过实例理解了平面区域的意义，并会画出平面区域，还能初步用数学关系表示简单的二元线性规划的限制条件，将实际问题转化成数学问题。从数学知识上看，问题涉及多个已知数据，多个字母变量、多个不等关系，从数学方法上看，学生对图解法的认识还很少，数形结合的思想方法的掌握还需时日，这成了学生学习的困难。

四、教学策略分析

本课以问题为载体，以学生为主体，以数学实验为手段，以问题解决为目的，激发学生动手操作、观察思考、猜想探究的兴趣。注重引导帮助学生充分体验“从实际问题到数学问题”的建构过程，“从具体到一般”的抽象过程。应用“数形结合”的思想方法，培养学生学会分析问题，解决问题的能力。

五、教学过程

教 学环 节

教学内容

师生互动

设计意图

一、回顾旧知

请同学们作出不等式组所表示的平面区域

请一位学生上黑板，按要求规范作图，老师巡视不仅起到温故的作用，同时为后引例中的可行域服务

二、提出问题激发热情

创设情境：

李咏主持的《非常6+1》是大家很喜欢的娱乐节目。为了提高更多收视率，央视准备为宣传《非常6+1》播放两套宣传片：其中宣传片甲播放时间为4分，其中广告时间为30秒，收视观众为60万，宣传片乙播放时间为2分钟，其中广告时间为1分钟，收视观众为10万。广告公司规定每周至少有3.5分钟广告，而电视台每周只能为该栏目宣传片提供不多于16分钟的节目时间，电视台每周应播放两套宣传片各多少次，才能使收视观众最多?

问题1：如何将生活问题转化为数学问题?

问题2：应设什么为变量？它们要满足什么关系？

问题3：转化为解决什么样的数学问题？

师：现在问题转化为已知x,y满足关系中

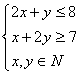
，求z=6x+y最值问题。

师:我们先来学习几个有关概念。

问题4：已知x,y满足条件

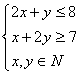
，求z=6x+y最值问题。

问题5：求最值有什么方法?

生：函数法、几何法

师：能否将双变量转化为单变量。

生：不能。没有x，y的等量关系。

师：那么能否从x,y满足的图形入手呢?

生：可以，x,y是平面区域上有限个点，可以将坐标代入求z值。

师：通过已经设置好的表格，完成最优解。

教师引导学生得出：设甲宣传片x次，乙宣传片y次，满足

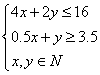
即

(1)

设收视观众人数为z(万人)，建立目标函数：

Z=6x+y,其中x,y满足不等式组(1)

教师介绍线性规划的有关概念，并启发学生思考如何解决最值问题，同时学生不断进行尝试。

问题情景使学生感到数学是自然的、有用的。

让学生经历实际问题抽象为数学问题的整个模型建立过程，体会数学源于生活，又服务于生活。

通过问题串将难点分解，同时将思维层层递进。

利用信息技术得到图解的特殊法—代点计算。

三、实验操作深入探究

问题6：这种方法有什么局限性?

生：它只能解决x,y有限个点的问题。

问题7：若将约束条件改成

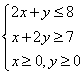
，求z=6x+y最值问题，我们应该如何解决?(学生思考)

问题8：你能从几何角度来研究z=6x+y吗?它对应图形是什么?

问题9： z的最值问题可以转化为求与直线有关的什么问题?

转化为：直线y=-6x+z在区域中变化时纵截距的最值问题。

师：几何画板动态演示，学生观察z值变化与截距关系。

问题10：纵截距的最大值是否一定是z的最大值