生：是（不是）

师：到底是不是，我们一起来研究下。( 学生操作几何画板，演示)提示：如果我们变换目标函数，那z值与纵截距的关系有什么变化。

问题11：通过演示你有什么发现?

问题12：z=ax+by，z与截距关系主要由哪个字母决定。

结论1：最优解通常在交点处取得。

2：z的最值问题可以转化为直线在y轴的截距问题。

将有限点上升到区域问题，体现特殊到一般的思想。

通过学生实验，老师几何画板的演示，以及师生不断探究归纳出Z最值问题可转化为直线纵截距的最值问题。

学生思维的最近发现区是上节的相关知识，教师有目的引导学生直观感知，操作确认，这样引导出教科书给出的数形结合的合理性。

四、例题展示规范答题

1.回归引例：

例1 已知x，y满足条件

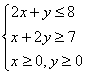
，求 Z=6x+y的最大值。

变式1.已知x，y满足条件

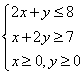
，求Z=6x-2y的最值。

小结：形如：Z=ax+by(b

0)的最值，即直线

在平面区域内有公共解　　　时，纵截距的最值。

备用题：

1.错在哪儿?

变式2.已知x，y满足条件

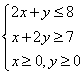
，设z=ax+y (a>0)，在(3,2)取最大值求a 取值范围。

变式3.(备用)已知x，y满足条件

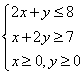
，设z=ax+y (a>0)，若Z取得最大值时对应点有无数个，求a 的值。

教师规范解题过程：解线性规划问题的步骤：画、移、求、答。

通过学生对变式1的练习教师的讲解，引导学生思考Z的最值与直线纵截距之间的关系。

教师展示变式训练1中的错误的解法，让学生发现错误。

备用题将学生的思维从动态的角度体会目标函数。

利用信息技术突破难点，得到引例的最终结论，这是本节课的中心所在。

通过例题的不断深入让学生进一步体会x、y的约束条件，以及几何法求最值的特点。

五、课堂小结、布置作业

(一)课堂小结：

以提问形式给出小结：

1、 解线性规划问题的一般步骤是什么?

(画—移—求—答)

2、目标函数z的最值问题可转化为直线在y轴上的截距的最值问题。

（二）作业布置：

1、书面作业：书P91 练习1、2

2、课外拓展:上网查阅有关线性规划的资料，了解它的实际应用。

学生自己思考，小结可写在自己的笔记本上，也可以口头交流，教师可引导学生进行小结

上文所提供的高三数学简单线性规划问题教案设计，大家看了之后是不是感觉很受用呢?希望大家对本网及时关注。

相关推荐：

人教A版高三数学一元二次不等式及其解法教案设计（第三单元）

人教A版高三数学二元一次不等式（组）教案设计（第三单元）