三、解答题(共9进大题，共90分)

16.解方程： 2 x + x x+3 =1.

★☆☆☆☆

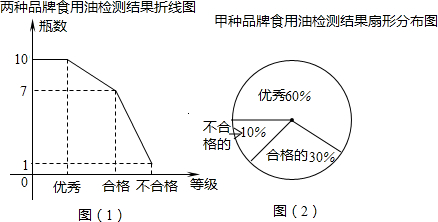
17.为了加强食品安全管理，有关部门对某大型超市的甲、乙两种品牌食用油共抽取18瓶进行检测，检测结果分成“优秀“、“合格“和“不合格”三个等级，数据处理后制成以下折线统计图和扇形统计图.

(1)甲、乙两种品牌食用油各被抽取了多少瓶用于检测?

(2)在该超购买一瓶乙品牌食用油，请估计能买到“优秀”等级的概率是多少?

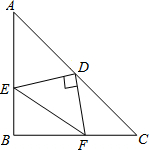
18.如图，在等腰直角三角形ABC中，∠ABC=90°，D为AC边上中点，过D点作DE丄DF，交AB于E，交BC于F，若AE=4，FC=3，求EF长.

VIP

19.有3张扑克牌，分別是红桃3、红桃4和黑桃5.把牌洗匀后甲先抽取一张，记下花色和数字后将牌放回，洗匀后乙再抽取一张.

(1)先后两次抽得的数字分别记为s和t，求|s-t|≥l的概率.

(2)甲、乙两人做游戏，现有两种方案.A方案：若两次抽得相同花色则甲胜，否则乙胜.B方案：若两次抽得数字和为奇数则甲胜，否则乙胜.请问甲选择哪种方案胜率更高?

20.今年我省干旱灾情严重，甲地急需抗旱用水15万吨，乙地13万吨.现有两水库决定各调出14万吨水支援甲、乙两地抗旱.从A地到甲地50千米，到乙地30千米;从B地到甲地60千米，到乙地45千米

(1)设从A水库调往甲地的水量为x万吨，完成下表：

甲 乙 总计

A x 14

B 14

总计 15 13 28

(2)请设计一个调运方案，使水的调运总量尽可能小.(调运量=调运水的重量×调运的距离，单位：万吨•千米)

VIP

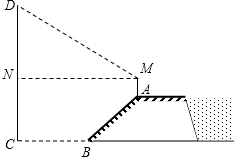
21.如图，防洪大堤的横断面是梯形，背水坡AB的坡比i=1：

3 (指坡面的铅直高度与水平宽度的比)，且AB=20m.身高为1.7m的小明站在大堤A点，测得髙压电线杆顶端点D的仰角为30°.已知地面CB宽30m，求髙压电线杆CD的髙度(结果保留三个有效数字，

3 ≈1.732).

VIP

22.如图，在圆内接四边形ABCD中，CD为∠BCA的外角的平分线，F为

AD 上一点，BC=AF，

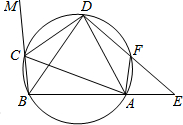
延长DF与BA的延长线交于E.

(1)求证：△ABD为等腰三角形.

(2)求证：AC•AF=DF•FE.

VIP

23.我市某镇的一种特产由于运输原因，长期只能在当地销售.当地政府对该特产的销售投资收益为：每投入x万元，可获得利润P=− 1 100 (x−60)2+41(万元).当地政府拟在“十二•五”规划中加快开发该特产的销售，其规划方案为：在规划前后对该项目每年最多可投入100万元的销售投资，在实施规划5年的前两年中，每年都从100万元中拨出50万元用于修建一条公路，两年修成，通车前该特产只能在当地销售;公路通车后的3年中，该特产既在本地销售，也在外地销售.在外地销售的投资收益为：每投入x万元，可获利润Q=− 99 100 (100−x)2+ 294 5 (100−x)+160(万元).

(1)若不进行开发，求5年所获利润的最大值是多少?

(2)若按规划实施，求5年所获利润(扣除修路后)的最大值是多少?

(3)根据(1)、(2)，该方案是否具有实施价值?

VIP

24.如图所示，过点F(0，1)的直线y=kx+b与抛物线y= 1 4 x2交于M(x1，y1)和N(x2，y2)两点(其中x1<0，x2>0).

(1)求b的值.

(2)求x1•x2的值.

(3)分别过M，N作直线l：y=-1的垂线，垂足分别是 M1和N1.判断△M1FN1的形状，并证明你的结论.

(4)对于过点F的任意直线MN，是否存在一条定直线m(m是常数)，使m与以MN为直径的圆

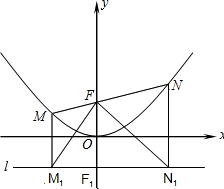
相切?如果有，请求出这条直线m的解析式;如果没有，请说明理由.

以上就是关于2011年湖北省随州市中考数学试题的全部内容，希望可以对正在面临中考的大家有所帮助!

相关推荐：

2013湖北随州中考语文模拟试题：深层次阅读 

2013随州中考语文模拟试题—文言文阅读