24.如图，在一个长40m、宽30m的长方形小操场上，王刚从A点出发，沿着A⇒B⇒C的路线以3m/s的速度跑向C地.当他出发4s后，张华有东西需要交给他，就从A地出发沿王刚走的路线追赶.当张华跑到距B地2 2 3 m的D处时，他和王刚在阳光下的影子恰好重叠在同一条直线上.此时，A处一根电线杆在阳光下的影子也恰好落在对角线AC上.

(1)求他们的影子重叠时，两人相距多少米?(DE的长)

(2)求张华追赶王刚的速度是多少?(精确到0.1m/s)

VIP

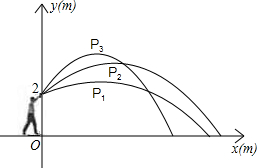
25.小明代表班级参加校运会的铅球项目，他想：“怎样才能将铅球推得更远呢”，于是找来小刚做了如下的探索：小明手挚铅球在控制每次推出时用力相同的条件下，分别沿与水平线成30°、45°、60°方向推了三次.铅球推出后沿抛物线形运动.如图，小明推铅球时的出手点距地面2m，以铅球出手点所在竖直方向为y轴、地平线为x轴建立直角坐标系，分别得到的有关数据如下表：

铅球的方向与水平线的夹角 300 450 600

铅球运行所得到的抛物线解析式  y1=-0.06(x-3)2+2.5  y2=

(x-4)2+3.6  y3=-0.22(x-3)2+4

估测铅球在最高点的坐标  P1(3，2.5)  P2(4，3.6)  P3(3，4)

铅球落点到小明站立处的水平距离  9.5m

m  7.3m

(1)请你求出表格中两横线上的数据，写出计算过程，并将结果填入表格中的横线上;

(2)请根据以上数据，对如何将铅球推得更远提出你的建议.

☆☆☆☆☆

26.我们常用各种多边形地砖铺砌成美丽的图案，也就是说，使用给定的某些多边形，能够拼成一个平面图形，既不留一丝空白，又不互相重叠，这在几何里叫做平面密铺(镶嵌).我们知道，当围绕一点拼在一起的几个多边形的内角的和为360°时，就能够拼成一个平面图形.某校研究性学习小组研究平面密铺的问题，其中在探究用两种边长相等的正多边形做平面密铺的情形时用了以下方法：

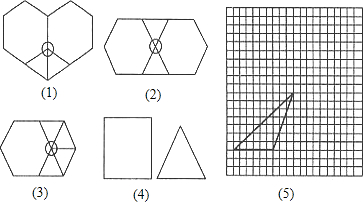
如果用x个正三角形、y个正六边形进行平面密铺，可得60°•x+120°•y=360°，化简得x+2y=6.因为x、y都是正整数，所以只有当x=2，y=2或x=4，y=1时上式才成立，即2个正三角形和2个正六边形或4个正三角形和1个正六边形可以拼成一个无缝隙、不重叠的平面图形，如图(1)、(2)、(3).

(1)请你仿照上面的方法研究用边长相等的x个正三角形和y个正方形进行平面密铺的情形，并按图(4)中给出的正方形和正三角形的大小大致画出密铺后图形的示意图(只要画出一种图形即可);

(2)如果用形状、大小相同的如图(5)方格纸中的三角形，能进行平面密铺吗?若能，请在方格纸中画出密铺的设计图.

27.如图(1)，已知圆O是等边△ABC的外接圆，过O点作MN∥BC分别交AB、AC于M、N，且MN=a.另一个与△ABC全等的等边△DEF的顶点D在MN上移动(不与点M、N重合)，并始终保持EF∥BC，DF交AB于点P，DE交AC于点Q.

(1)试判断四边形APDQ的形状，并进行证明;

(2)设DM为x，四边形APDQ的面积为y，试探究y与x的函数关系式;四边形APDQ的面积能取到最大值吗?如果能，请求出它的最大值，并确定此时D点的位置.

(3)如图(2)，当D点和圆心O重合时，请判断四边形APDQ的形状，并说

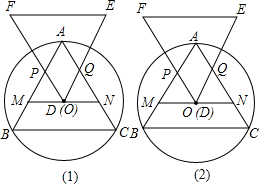
明理由;你能发现四边形APDQ的面积与△ABC的面积有何关系吗?为

希望小编的这篇山东省2005年济南市中考数学试卷(课标卷)能够解大家的燃眉之急，精品学习网在此预祝大家中考顺利!

相关推荐：

山东2008年济南市中考数学试题解答题练习  

2008年山东省济南市中考数学试题（填空题）