20.先化简，再求值：( 1 a+2 −1)÷ a2−1 a+2 ，其中a=2.

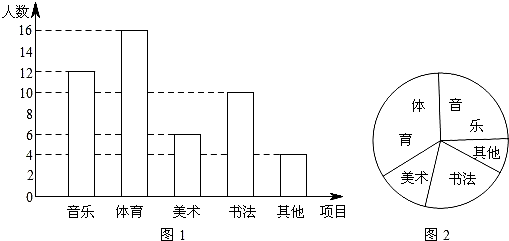
21.为了解某学校学生的个性特长发展情况，在全校范围内随机抽查了部分学生参加音乐、体育、美术、书法等活动项目(每人只限一项)的情况.并将所得数据进行了统计.结果如图1所示.

(1)在这次调查中，一共抽查了 名学生;

(2)求出扇形统计图(图2)中参加“音乐活动”项目所对扇形的圆心角的度数;

(3)若该校有2400名学生，请估计该校参加“美术活动项目的人数.

22.为落实素质教育要求，促进学生全面发展，我市某中学2009年投资11万元新增一批电脑，计划以后每年以相同的增长率进行投资，2011年投资18.59万元

(1)求该学校为新增电脑投资的年平均增长率;

(2)从2009年到2011年，该中学三年为新增电脑共投资多少万元?

VIP

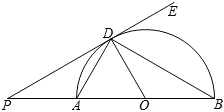
23.如图，AB是半圆的直径，O为圆心，AD、BD是半圆的弦，且∠PDA=∠PBD.

(1)判断直线PD是否为⊙O的切线，并说明理由;

(2)如果∠BDE=60°，PD=

3 ，求PA的长.

24.某中学九年级甲、乙两班商定举行一次远足活动，A、B两地相距10千米，甲班从A地出发匀速步行到B地，乙班从B地出发匀速步行到A地.两班同时出发，相向

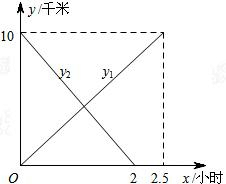
而行.设步行时间为x小时，甲、乙两班离A地的距离分别为y1、y2千米，y1、y2与x的函数关系图象如图所示.根据图象解答下列问题：

(1)直接写出，y1、y2与x的函数关系式;

(2)求甲、乙两班学生出发后，几小时相遇?相遇时乙班离A地多少千米?

(3)甲、乙两班首次相距4千米时所用时间是多少小时?

VIP

25.如图1，已知矩形ABED，点C是边DE的中点，且AB=2AD.

(1)判断△ABC的形状，并说明理由;

(2)保持图1中△ABC固定不变，绕点C旋转DE所在的直线MN到图2中(当垂线段AD、BE在直线MN的同侧)，试探究线段AD、BE、DE长度之间有什么关系?并给予证明;

(3)保持图2中△ABC固定不变，继续绕点C旋转DE所在的直线MN到图3中的位置(当垂线段AD、BE在直线MN的异侧).试探究线段AD、BE、DE长度之间有什么关系?并给予证明.

26.如图：二次函数y=-x2+ax+b的图象与x轴交于A(- 1 2 ，0)，B(2，0)两点，且与y轴交于

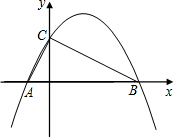
点C.

(1)求该抛物线的解析式，并判断△ABC的形状;

(2)在x轴上方的抛物线上有一点D，且A、C、D、B四点为顶点的四边形是等腰梯形，请直接写出D点的坐标;

(3)在此抛物线上是否存在点P，使得以A、C、B、P四点为顶点的四边形是直角梯形?若存在，求出P点的坐标;若不存在，说明理由.

由精品小编为大家提供的山东省2010年临沂市中考数学试题就到这里了，希望可以帮助到您!

相关推荐：

2012年山东省临沂市中考物理试卷 

2010年山东省临沂市中考化学试卷