应用迁移巩固提高

例1.如图，E是正方形ABCD中CD边上任意一点，以点A为中心，把△ADE顺时针旋转90°.

(1)画出旋转后的图形.

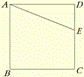
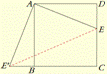
(2)连接EE′， 则△AEE′是怎样的三角形?

教师提问：想要作出旋转后的图形，关键是确定哪几个点的对应点?

学生指出关键是确定决定△ADE形状、大小的三个顶点的对应点.

教师关注：

学生是否把握住图形旋转的实质.

教师提问：你能用多种方法确定E′点吗?

学生小组讨论，并利用投影仪展示自己的作图方法.

教师关注：

(1)学生能否灵活运用旋转的性质，运用不同的方法作图.

(2)学生的语言表达是否准确.

学生自主作答，说清理由.

教师关注：

(1)学生对旋转性质及等腰直角三角形的掌握情况.

(2)学生的语言表达是否准确.

检测学生是否把握住图形旋转的实质：图形的旋转可看作是点的旋转，而作出旋转后的图形关键是作出决定图形形状、大小的几个关键点的对应点.

让学生探讨确定点E′的不同方法，考查学生能否灵活运用旋转的性质，体现了“一题多解”，很好地训练了学生思维的灵活性和发散性，充分调动了学生学习的积极性.

学生利用投影仪展示自己的探究成果，培养学生语言表达及胆量.

考查学生对旋转性质及等腰直角三角形的掌握情况，锻炼学生的语言表达能力.

教学

环节

问题与情境

师生行为

设计意图

 

 

 

应用迁移巩固提高

变式一：如果把△ADE旋转的方向改为逆时针，你会画出旋转后的图形吗?

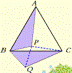
变式二：如图：P是等边△ABC内的一点，把△ABP通过旋转得到△BQC.

(1)指出旋转中心、旋转方向和旋转角度?

(2)连接PQ，则△BPQ是怎样的三角形?

(3)若PA=5，PC=4，PB=3，则△PQC是怎样的三角形?

(留作课后作业)

 

学生自主作答.

教师关注：

(1)学生对旋转概念和性质的掌握情况.

(2)学生对于正三角形、勾股定理逆定理的掌握情况.

(3)学生的语言表达是否准确.

巩固图形旋转的作图;体会规定旋转方向的意义.

考查学生对旋转概念、性质，正三角形的判定，勾股定理的逆定理的掌握情况.

进行变式训练，体现了“一题多变”的思想. 在正方形中将图形旋转90°、在正三角形中将图形旋转60°是常见的旋转技巧，这儿的渗透为今后利用这种旋转技巧解题作铺垫.

 

自主

练习

深化

新知

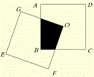
如图正方形EFOG绕与之边长相等的正方形ABCD的中心O旋转任意角度，问：图中阴影部分的面积与正方形ABCD的面积有什么关系?

学生自主作答，上讲台展示.

教师关注：

(1)学生能否连接恰当的辅助线.

(2)学生能否利用割补的方法，将阴影部分的面积转化成等腰直角三角形或正方形来求解.

(3)学生能否用不同的方法解答.

考查学生对旋转性质、三角形全等、正方形的性质等知识的掌握情况.

培养学生转化的思想，锻炼学生的发散思维.

畅谈收获归纳

总结

利用数学日记的形式，师生共同进行小结.

学生小结：自主小结和交流知识学习的收获，过程经历的感受，数学思想的感悟，学习方法的体会等，或提出疑问进行讨论;

教师小结：帮助学生整理所学知识，引导学生进一步体会探究学习的过程和方法，领会数学的思想.

小结是知识的完善和方法的提升.而学生在小结时可能只注重于知识小结忽略了方法的总结，教师要适时帮助，让学生养成良好的学习数学的方法和习惯.

数学日记很好地反映每一个学生的情况，体现了面向每一个学生的新课程理念.

视频欣赏

 

学生感受到旋转在生活中无处不在.

与导入呼应，体会到数学来源于生活又应用于生活，体会数学的应用价值.

布置作业拓展延伸

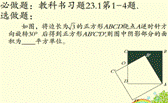
学生课后独立完成.

巩固新知，检测学生对于新知的掌握情况，为下一节新课的学习作铺垫.

分层布置作业，以适应不同梯度学生的需求.

 

板书设计

大家对与上文小编为大家准备的初青岛版数学初三上册图形的旋转教案模板仔细品味了吗?希望大家喜欢，更多相关内容请关注精品学习网。

相关推荐：

青岛版数学初三上册图形的平移教案模板：第二章  

青岛版初三数学中位线定理教案设计：上册