●忽视隐含条件，导致结果错误。

【例2】

(1) 设

是方程

的两个实根，则

的最小值是

思路分析 本例只有一个答案正确，设了3个陷阱，很容易上当。

利用一元二次方程根与系数的关系易得：

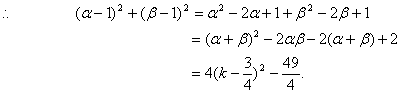
有的学生一看到

，常受选择答案(A)的诱惑，盲从附和。这正是思维缺乏反思性的体现。如果能以反思性的态度考察各个选择答案的来源和它们之间的区别，就能从中选出正确答案。

原方程有两个实根

，∴

T

当

时，

的最小值是8;

当

时，

的最小值是18。

这时就可以作出正确选择，只有(B)正确。

(2) 已知(x+2)2+ =1, 求x2+y2的取值范围。

错解 由已知得 y2=-4x2-16x-12，因此 x2+y2=-3x2-16x-12=-3(x+

)2+

，

∴当x=-时，x2+y2有最大值，即x2+y2的取值范围是(-∞, ]。

分析 没有注意x的取值范围要受已知条件的限制，丢掉了最小值。

事实上，由于(x+2)2+ =1 T (x+2)2=1- ≤1 T -3≤x≤-1，

从而当x=-1时x2+y2有最小值1。∴ x2+y2的取值范围是[1, ]。

注意有界性：偶次方x2≥0，三角函数-1≤sinx≤1，指数函数ax>0，圆锥曲线有界性等。